Leetcode个人笔记-medium

一月 10, 2024 17918

随便刷刷

动态规划

动规是由前一个状态推导出来的，而贪心是局部直接选最优的

维数相当于需要的状态的个数？

对于动态规划问题，我将拆解为如下五步曲

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

写代码之前

推导状态转移方程
把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。
debug: 找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

121. 买卖股票的最佳时机

贪心

因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润。

时间复杂度O()

for (int i = 0; i < prices.size(); i++) {
     low = min(low, prices[i]);  // 取最左最小价格
     result = max(result, prices[i] - low); // 直接取最大区间利润
 }

动态规划

动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i][0] 表示第i天持有股票所得最多现金，这里可能有同学疑惑，本题中只能买卖一次，持有股票之后哪还有现金呢？

其实一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]，这是一个负数。

dp[i][1] 表示第i天不持有股票所得最多现金

注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态

很多同学把“持有”和“买入”没区分清楚。

在下面递推公式分析中，我会进一步讲解。

确定递推公式

如果第i天持有股票即dp[i][0]，那么可以由两个状态推出来

第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]

那么dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);

如果第i天不持有股票即dp[i][1]，也可以由两个状态推出来

第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

这样递推公式我们就分析完了

dp数组如何初始化

由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出

其基础都是要从dp[0][0]和dp[0][1]推导出来。

那么dp[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] -= prices[0];

dp[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0;

确定遍历顺序

从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历。

举例推导dp数组

以示例1，输入：[7,1,5,3,6,4]为例，dp数组状态如下：

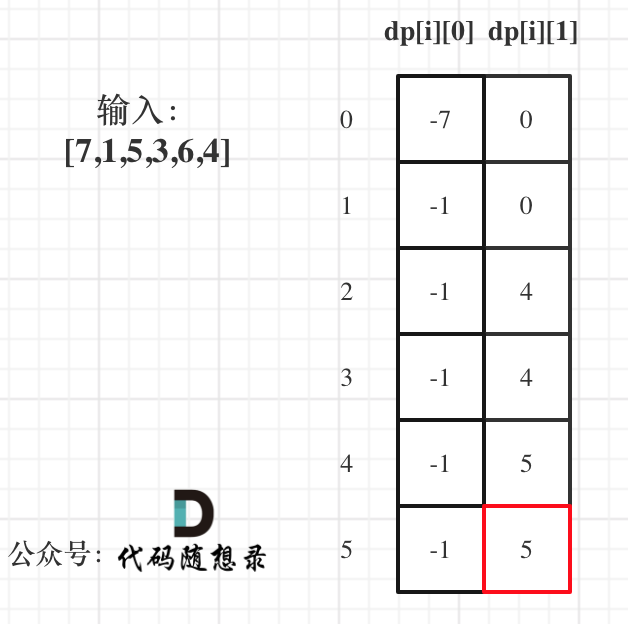image

1997. 访问完所有房间的第一天

前缀和优化

通过前缀和，我们可以把连续子数组的元素和转换成两个前缀和的差

前缀和大小比原数组大1
时间复杂度：初始化 O(n)。其中n为 nums的长度。
空间复杂度：O(n)

Untitled)

取mod技巧

在for中取模，防止爆long

1	`x = (x + MOD) % MOD; // + MOD 避免算出负数`

70. 爬楼梯

动规五部曲：

定义一个一维数组来记录不同楼层的状态

确定dp数组以及下标的含义
1. dp[i]：爬到第i层楼梯，有dp[i]种方法
确定递推公式
1. 所以dp[i] = dp[i - 1] + dp[i - 2] 。在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性！
初始化
1. 不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2
确定遍历顺序
1. 从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的
举例推导dp数组
1. 如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。

拓展

这道题目还可以继续深化，就是一步一个台阶，两个台阶，三个台阶，直到 m个台阶，有多少种方法爬到n阶楼顶。

这其实是一个完全背包问题

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) { // 把m换成2，就可以AC爬楼梯这道题
                if (i - j >= 0) dp[i] += dp[i - j];
            }
        }
        return dp[n];
    }
};

0-1背包

最简单的是推导公式了，推导公式估计看一遍就记下来了

难在如何初始化
难在遍历顺序

代码模版

void test_2_wei_bag_problem1() {
    vector<int> weight(n, 0); // 存储每件物品所占空间
    vector<int> value(n, 0);  // 存储每件物品价值
    for(int i = 0; i < n; ++i) {
        cin >> weight[i];
    }
    for(int j = 0; j < n; ++j) {
        cin >> value[j];
    }
    bagweight  = max(weight) // 伪代码
    // dp数组, dp[i][j]代表行李箱空间为j的情况下,从下标为[0, i]的物品里面任意取,能达到的最大价值
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化, 因为需要用到dp[i - 1]的值
    // j < weight[0]已在上方被初始化为0
    // j >= weight[0]的值就初始化为value[0]
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
        for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
            // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            // 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值
            // 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
    cout << dp[weight.size() - 1][bagweight] << endl;
}

遍历方向如何判断？

要理解递归的本质和递推的方向。

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。

dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正上方向），那么先遍历物品，再遍历背包的过程如图所示：

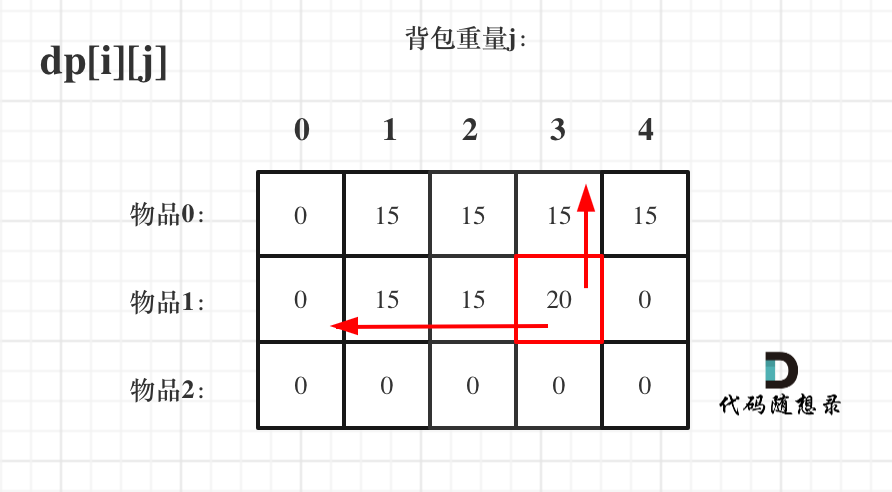image

再来看看先遍历背包，再遍历物品呢，如图：

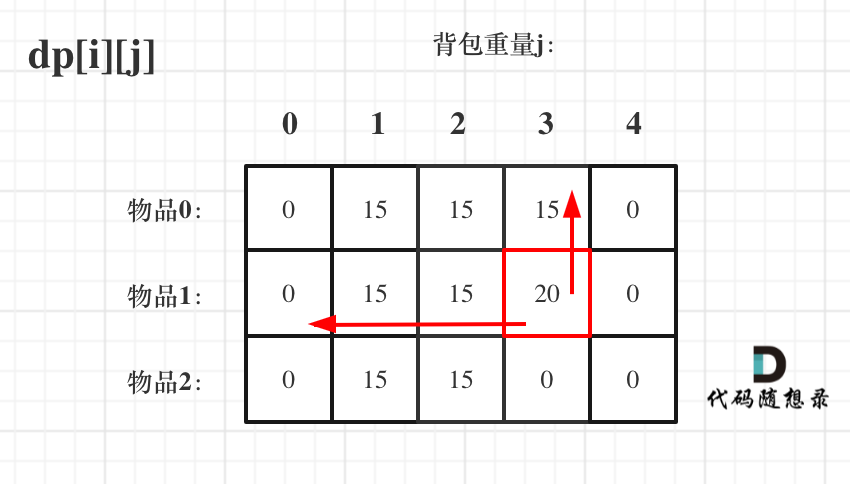image

可以看出，虽然两个for循环遍历的次序不同，但是dp[i][j]所需要的数据就是左上角，根本不影响dp[i][j]公式的推导！

其他变体，就不一定都行了，得看数据是否在左上角

完全背包

多重背包

递归

递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数。

int function3(int x, int n) {
    if (n == 0) return 1;
    if (n == 1) return x;

    if (n % 2 == 1) {
        return function3(x, n / 2) * function3(x, n / 2)*x;
    }
    return function3(x, n / 2) * function3(x, n / 2);
}

Untitled)

这棵满二叉树的节点数量就是2^3 + 2^2 + 2^1 + 2^0 = 15。时间复杂度忽略掉常数项-1之后，这个递归算法的时间复杂度依然是O(n)

int function4(int x, int n) {
    if (n == 0) return 1;
    if (n == 1) return x;
    int t = function4(x, n / 2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t * t * x;
    }
    return t * t;
}

依然还是看他递归了多少次，可以看到这里仅仅有一个递归调用，且每次都是n/2 ，所以这里我们一共调用了log以2为底n的对数次。

**每次递归了做都是一次乘法操作，这也是一个常数项的操作，那么这个递归算法的时间复杂度才是真正的O(logn)**。

数组

C++中二维数组在地址空间上是连续的。

Java的二维数组可能是如下排列的方式：

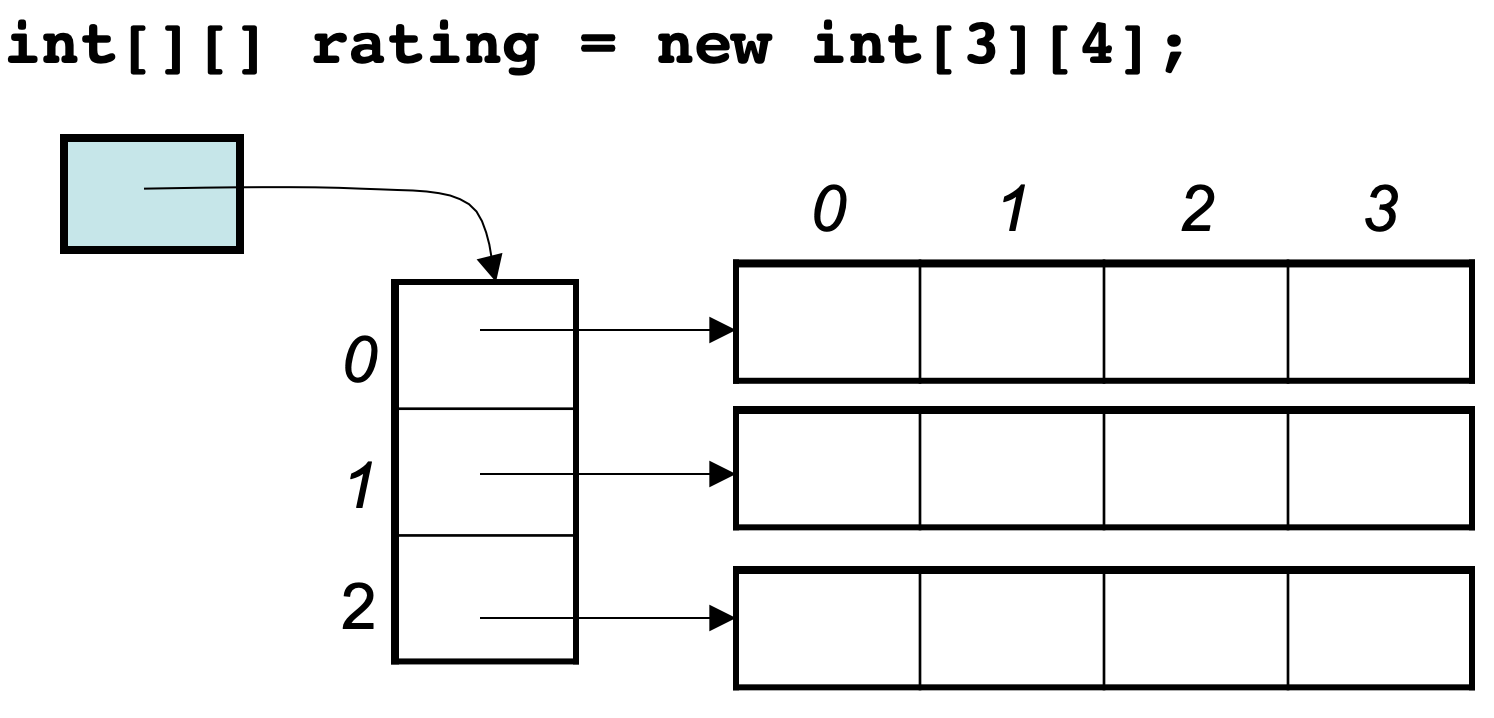image

704.二分查找

前提是数组为有序数组，同时题目还强调数组中无重复元素

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

1	`int middle = left + ((right - left) / 2);// 防止溢出等同于(left + right)/2`

209.长度最小的子数组

滑动窗口经典题

O（N)时间

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

双指针法的一种
思考：如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。
- 窗口内是什么？
- 如何移动窗口的起始位置？
- 如何移动窗口的结束位置？

while后不要加分号’;’ ！！！

54.遍历螺旋矩阵

59. 螺旋矩阵 II

1
2
3

// vector前插与后插
matrix.insert(matrix.begin(),empty1);
matrix.push_back(empty2);

思路1：填充0，遇到0则转弯

容错率高

思路2：定义当前左右上下边界 l,r,t,b. 四个for循环，每个循环后调整边界

效率高

思路3：四个for循环，每个循环后n-2。套圈思维。奇偶分开处理

前缀和

处理子串

处理非顺序数组

处理区间和

560. 和为 K 的子数组

前缀和 + 哈希表优化

构建前缀和数组，以快速计算区间和；
由于只关心次数，不关心具体的解，我们可以使用哈希表加速运算；

链表

203.移除元素

养成手动清理内存的习惯。

malloc

头结点如何移除

将头结点向后移动一位就可以

逻辑统一化

添加虚拟头结点，则不用分类

```cpp
ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
```

空节点处理

while(fast != NULL && fast->next != NULL)

19.删除链表的倒数第N个节点

双指针法。适用于寻找距离尾部第k个节点、寻找环入口、寻找公共尾部入口等。

同样可以添加虚拟头结点

最后 return dummyHead->next;

while代替for

```cpp
while(n-- && fast != NULL) {
            fast = fast->next;
        }
```

142.环形链表II

方法一：哈希表

一个非常直观的思路是：我们遍历链表中的每个节点，并将它记录下来；一旦遇到了此前遍历过的节点，就可以判定链表中存在环。借助哈希表可以很方便地实现。
O（n）空间，O(n)速度

方法二：快慢指针

我们使用两个指针，它们起始都位于链表的头部。slow指针每次向后移动一个位置，而 fast指针向后移动两个位置。如果链表中存在环，fast指针最终将再次与 slow指针在环中相遇。
数学计算可知，x=z
O（1）空间，O(n)速度

哈希表

哈希法是牺牲了空间换取了时间
遇到需要判断一个元素是否出现过的场景应该第一时间想到哈希法！

在C++中，set 和 map 分别提供以下三种数据结构，其底层实现以及优劣如下表所示：

集合	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(logn)	O(logn)
std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。

映射	底层实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::map	红黑树	key有序	key不可重复	key不可修改	O(logn)	O(logn)
std::multimap	红黑树	key有序	key可重复	key不可修改	O(log n)	O(log n)
std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。

当我们要使用集合来解决哈希问题的时候，优先使用unordered_set，因为它的查询和增删效率是最优的，如果需要集合是有序的，那么就用set，如果要求不仅有序还要有重复数据的话，那么就用multiset。

242.有效的字母异位词

判断字符个数，可以映射字符到26长度的数组（即哈希表）

也可使用unordered_map

1. 两数之和

本题其实有四个重点：

为什么会想到用哈希表
哈希表为什么用map
本题map是用来存什么的
- 访问过的数组
map中的key和value用来存什么的
- 方便查下标

什么时候使用哈希法

当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

两数之和这道题目，不仅要判断y是否存在而且还要记录y的下标位置，因为要返回x 和 y的下标。所以set 也不能用。map最合适

数组的大小是受限制的，而set元素很少，哈希值太大会造成内存空间的浪费。
这道题目中并不需要key有序，选择std::unordered_map 效率更高！

15. 三数之和

排序，方便去重

1	`sort(nums.begin(),nums.end());`

使用哈希法，N^2可行。但最大问题在于去重细节多
使用双指针法，同样N^2，但更容易去重，原因是排序后指针的移动非常方便。而哈希需要单独判断，并且b和c元素的顺序混乱

防止越界

数组迭代去重，尽量使用num[i-1]而不是i+1
所有取数组操作前/对索引加减后，都判断是否越界（如nums[right+1]前，判断right!=len-1）

字符串

344.反转字符串

双指针法

如果题目关键的部分直接用库函数就可以解决，建议不要使用库函数。

不了解库函数时间复杂度

如果库函数仅仅是解题过程中的一小部分，并且你已经很清楚这个库函数的内部实现原理的话，可以考虑使用库函数。

541. 反转字符串II

固定规律，用for

当需要固定规律一段一段去处理字符串的时候，可以在for循环的表达式上做做文章。

151.翻转字符串里的单词

学会分解步骤

O(1)空间法

移除多余空格
- 双指针法，把fast的字符移到slow前端，手动添加空格。最后resize(slow)
将整个字符串反转
将每个单词反转

双指针法：

移除多余空格
从最后开始扫描单词
遇到空格，调整指针添加新字符串

28.实现strStr()

所以整个KMP算法的时间复杂度是O(n+m)的。其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，不需要回退。之前还要单独生成next数组，时间复杂度是O(m)。
暴力的解法因为每次都要回退，是O(n × m)，所以KMP在字符串匹配中极大地提高了搜索的效率。

KMP算法

KMP主要应用在字符串匹配上。

KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

如何记录已经匹配的文本内容，是KMP的重点：next数组

next数组就是一个前缀表（prefix table）。

前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。
前缀表

记录下标i之前（包括i）的字符串中，有多大长度的最长公共前后缀
- 最长公共前后缀定义：长度为前1个字符的子串a，最长相同前后缀的长度为0。长度为前2个字符的子串aa，最长相同前后缀的长度为1。长度为前3个字符的子串aab，最长相同前后缀的长度为0。

本质上：当不匹配时，待匹配串回到前缀末端，匹配串继续前行（后缀已与公共前缀匹配）

举一个例子：

要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。
下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀和后缀字符串是子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

image
找到的不匹配的位置，那么此时我们要看它的前一个字符的前缀表的数值是多少。
前一个字符的前缀表的数值是2，所以把下标移动到下标2的位置继续比配。可以再反复看一下上面的动画。

next数组的构建

构建和匹配非常相似，

本质上都是当不匹配时待匹配串回到前缀末端，匹配串继续前行（后缀已与公共前缀匹配）
- 求next过程实际上是dp（动态规划），只与前一个状态有关：
- 若不匹配，一直往前退到0或匹配为止
- 若匹配，则将之前的结果传递：
- 因为之前的结果不为0时，前后缀有相等的部分，所以next[j]所指的实际是与当前值相等的前缀，可视为将前缀从前面拖了过来，就不必将指针从初始开始匹配了，所以之前的结果是可以传递的。

void getNext(int* next, const string& s) {
       int j = 0;
       next[0] = 0;
       for(int i = 1; i < s.size(); i++) {
           while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
               j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
           }
           if (s[i] == s[j]) {
               j++;
           }
           next[i] = j;
       }
   }

模式串匹配文本串的整体代码如下：

int j = 0;
for (int i = 0; i < haystack.size(); i++) {
    while(j > 0 && haystack[i] != needle[j]) {
        j = next[j - 1];
    }
    if (haystack[i] == needle[j]) {
        j++;
    }
    if (j == needle.size() ) {
        return (i - needle.size() + 1);
    }
}

while 是为了回退直到前后缀一致

459.判断重复字符子串

解法1：字符串复制，判断新字符串内是否存在原字符串

等价转化思维
判断新字符串内是否存在原字符串时，可使用KMP,或是find函数

解法2：构造next公共前后缀表

若next[len-1]不为0，且公共前缀能被len整除，说明存在重复子串
等价转化思维。证明用到string位置间的相等转化
Untitled)

双指针

两个指针在一个for循环下完成两个for循环的工作

形式多样

快慢指针
正向指针负向指针

除了链表一些题目一定要使用双指针，其他题目都是使用双指针来提高效率，一般是将O(n^2)的时间复杂度，降为O(n)

栈与队列

队列是先进先出，栈是先进后出。

常用方法：

// 栈：
stack<int> s;
s.push(1);
s.push(2);

s.pop(); // 2 被弹出

int top_element = s.top(); // top_element = 1

if (s.empty()) {
  // 栈为空
}

size_t size = s.size(); // size = 1

stack<int> s1, s2;
s1.push(1);
s1.push(2);
s2.push(3);
s2.push(4);

s1.swap(s2); // 交换

// 现在 s1 中包含元素 3 和 4，s2 中包含元素 1 和 2

队列：先进先出

queue<int> q;
q.push(1);
q.push(2);

q.pop(); // 1 被弹出

// 3. front(): 返回队列首部元素，但不弹出。
int front_element = q.front(); // front_element = 1

// 4. back(): 返回队列尾部元素，但不弹出。
int back_element = q.back(); // back_element = 2

if (q.empty()) {
  // 队列为空
}

size_t size = q.size(); // size = 1

底层：

队列、栈是以底层容器完成其所有的工作，对外提供统一的接口
- 底层容器是可插拔的（也就是说我们可以控制使用哪种容器来实现栈的功能）。
所以STL中栈往往不被归类为容器，而被归类为container adapter（容器适配器）。

1	`![Untitled](<https://prod-files-secure.s3.us-west-2.amazonaws.com/56ceba07-d0ed-41cb-8031-a7aca0da9c79/86e838ef-c64f-4fad-b638-c1aaf8971e6a/Untitled.png)>)`

默认是deque。我们也可以指定vector为栈的底层实现，初始化语句如下：
- std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈
- std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列

232. 用栈实现队列

双栈模拟，in与out栈

本质：每次倒腾，顺序相反，考虑push做文章
关键：保持顺序。
- 关键在于把数据从输入栈倒入输出栈的条件是输出栈为空，这样就维持了输出栈顶是队列开头的定义，pop与peek不会出错

bug:

while (!inStack.empty()) 而不是for(int i=0;i<in.size();)
//size是动态的，不建议用

225. 用队列实现栈

本质：每次倒腾，顺序不变。所以考虑pop做文章
解法：一个队列在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素外）重新添加到队列尾部，此时再去弹出元素就是栈的顺序了。

20. 有效的括号

分析很重要，代码要囊括所有情况：有哪几种不匹配的情况

第一种情况，字符串里左方向的括号多余了，所以不匹配。

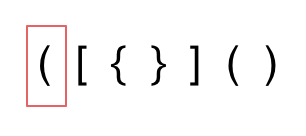image
第二种情况，括号没有多余，但是括号的类型没有匹配上。

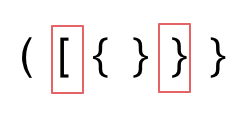image
第三种情况，字符串里右方向的括号多余了，所以不匹配。

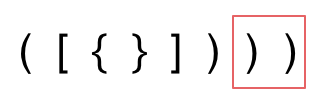image

单调栈

739. 每日温度

压栈可以压index，不一定压数据。map<int,int>的替代方案

我怎么能想到用单调栈呢？什么时候用单调栈呢？

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。
单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，

在使用单调栈的时候首先要明确如下几点：

单调栈里存放的元素是什么？

单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。

单调栈里元素是递增呢？还是递减呢？(顺序的描述为从栈头到栈底的顺序)

如果求一个元素右边第一个更大元素，单调栈就是递增的，如果求一个元素右边第一个更小元素，单调栈就是递减的。

加入T[6]，需要将栈里的T[5]，T[2]弹出

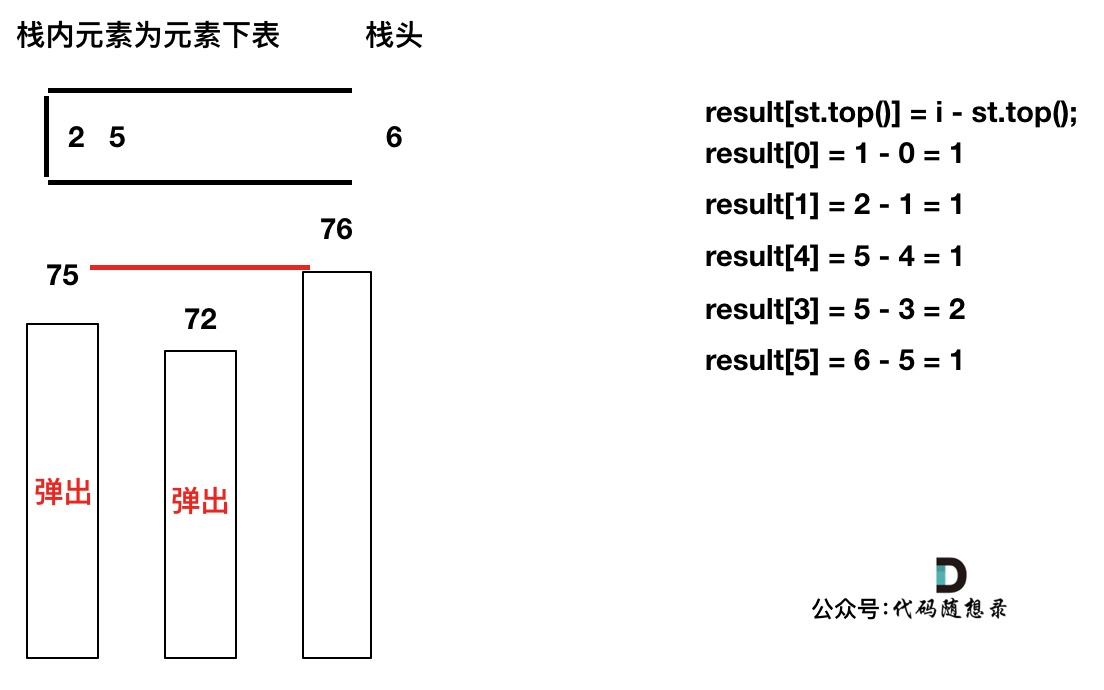image

同理，继续弹出

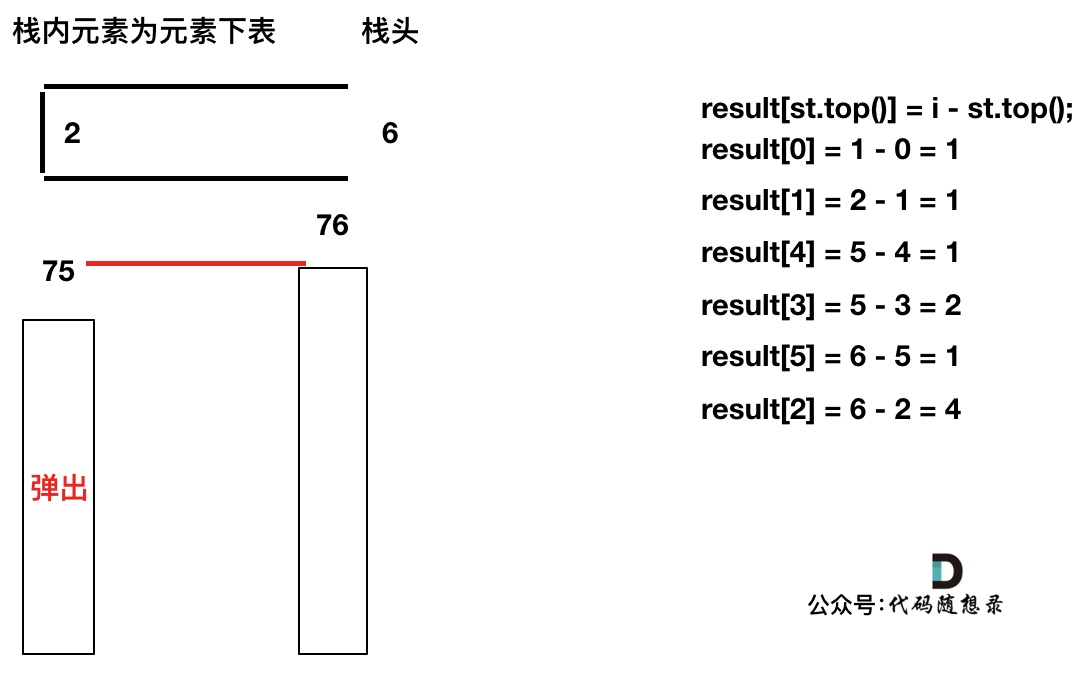image

496.下一个更大元素 I

没有重复元素，我们就可以用map哈希表来做映射了
求每个元素下一个比当前元素大的元素的位置，用单调栈。

push索引下标和值都可以。看输出要求。

索引更通用，但会慢

时间复杂度: O(m＋n)，其中 m是nums1的长度，n是nums2的长度。我们需要遍历nums2以计算nums2中每个元素右边的第一个更大的值;需要遍历nums1以生成查询结果。

503.下一个更大元素II

单调栈思路一样。

本篇我侧重说一说如何处理循环数组。

法1：更优雅
- for (int i = 1; i < nums.size() * 2; i++) 之后的i都变成i % nums.size()
法2：似乎更快
- 作标志位判断。只用取余count次

42. 接雨水

自己写过了！

暴力解法：

按列计算。雨水高度为min(lHeight, rHeight) - height。
- 注意lHeight和rHeight是最远的，不是最近的
- 每一列sum+=雨水高度-height
Untitled)

20210402091208445.png))

单调栈

为什么用？

与左右找第一个最小/最大有关，找每个柱子左右两边第一个大于该柱子高度

1.判断单调顺序

从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了
- 如果从大到小，只能判断出突出山峰在哪儿
栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

2.考虑相同处理

如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

3.栈里要保存什么数值

使用单调栈，也是通过长 * 宽 , 按行来计算雨水面积的。

长就是通过柱子的高度来计算，宽是通过柱子之间的下标来计算，
栈里就存放下标就行，想要知道对应的高度，通过height[stack.top()] 就知道弹出的下标对应的高度了。

while (!st.empty() && height[i] > height[st.top()]) { // 这里是while,往回计算行直到找到更高的
    int mid = st.top(); // 最低点。处理涉及栈中前两个元素和栈外一个元素
    st.pop();
    if (!st.empty()) {
        int h = min(height[st.top()], height[i]) - height[mid];
        int w = i - st.top() - 1; // 注意减一，只求中间宽度
        sum += h * w;
    }
}
st.push(i);

Untitled)

双指针

每到一个柱子都向两边遍历一遍，这其实是有重复计算的。

我们把每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight），这样就避免了重复计算。

区分：找最远的max还是最近的max

```cpp
      for(int i=1;i<len;i++){
          int left = i-1;
          while(left>=0 && height[left]<=height[i]){
              left = maxLeft[left];
          }
          maxLeft[i] = left; //跳跃找最近的max
      }

      
      for(int i=1;i<len;i++){
          int left = i-1;
          maxLeft[i] = max(maxLeft[left],height[i]); // 找最远的max
      }
```

84. 柱状图中最大的矩形

暴力解法：以单个矩形为基准，暴力向两边延伸

可以先写暴力找思路
看到时间复杂度为 O(N2) 和空间复杂度为 O(1)的组合，就可以考虑怎么空间换时间

双指针

双指针解法：同样思路的优化

两层for —> 先记录后计算
同样两层for，但向左遍历时跳跃，速度极大加快
- 必须记录在数组，才能跳跃

//记录每一个柱子，向左的 第一个更小 的下标
minLeft[0] = -1; // 哨兵
for(int i=1;i<len;i++){
    int left = i-1;
    while(left>=0 && heights[left]>=heights[i]){
        left = minLeft[left];//跳着找，更快。类似KMP
    }
    minLeft[i] = left;
}

int res = 0;
for(int i=0;i<len;i++){
    res = max(res,heights[i]*(minRight[i]-minLeft[i]-1));
}

单调栈

暴力解法的优化，

42. 接雨水 (opens new window)是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子。所以从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！

为什么用单调栈

任何一个长方体，要满足

向左右不能再延伸

的条件，即左右矩形要更小
- 与左右最大/最小值有关
- 在缓存数据的时候是从左向右缓存的，计算出一个结果的顺序是从右向左的，并且计算完成以后我们就不再需要了，符合后进先出的特点。因此，我们需要的这个作为缓存的数据结构就是栈。

怎么求

栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度

while (!st.empty() && heights[i] < heights[st.top()]) { // 注意while，遍历某一右边界对应的所有左边界。i++为调整右边界
    int mid = st.top(); // 中间的最小高度
    st.pop();
    if (!st.empty()) {
        int left = st.top();
        int right = i;
        int w = right - left - 1;
        int h = heights[mid];
        result = max(result, w * h);
    }
}

哨兵

考虑两种特殊的情况：

弹栈的时候，栈为空；
遍历完成以后，栈中还有元素；

为此可以我们可以在输入数组的两端加上两个高度为 0 （或者是 0.5，只要比 1 严格小都行）的柱形，可以回避上面这两种分类讨论。这两个站在两边的柱形有一个很形象的名词，叫做哨兵（Sentinel）。

如果数组本身是降序的，例如 [8,6,4,2]，在 8 入栈后，6 开始与8 进行比较，此时我们得到 mid（8），rigt（6），但是得不到 left。

堆

215. 数组中的第K个最大元素

堆解法

时间复杂度：O(nlog⁡n)

建堆的时间代价是 O(n)
- 复杂度分析并不是简单相乘：8.2 建堆操作 - Hello 算法 (hello-algo.com)
Untitled)
删除的总代价是 O(klog⁡n)
因为 k<n，故渐进时间复杂为 O(n+klog⁡n)=O(nlog⁡n)

空间复杂度：O(log⁡n)O(\log n)O(logn)，即递归使用栈空间的空间代价。

建堆

Untitled)

void maxHeapify(vector<int>& a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a[i], a[largest]);
            maxHeapify(a, largest, heapSize); //向子节点递归
        }
    }

    void buildMaxHeap(vector<int>& a, int heapSize) {
        for (int i = heapSize / 2; i >= 0; --i) {
            maxHeapify(a, i, heapSize); // 处理i个元素与其子女为大根堆
        } 
    }

删除堆顶

Untitled)

int findKthLargest(vector<int>& nums, int k) {
    int heapSize = nums.size();
    buildMaxHeap(nums, heapSize);
    for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
        swap(nums[0], nums[i]); //除堆顶
        --heapSize;
        maxHeapify(nums, 0, heapSize); // 递归重排
    }
    return nums[0];
}

桶排序解法

复杂度O(n)，要求数字值不能太大

在一般情况下，桶排序的时间复杂度为O(N + K)，具体解释如下：

桶的创建和元素分配（线性时间复杂度）：创建桶数组的时间复杂度为O(K)，遍历输入数组将元素分配到各个桶中的时间复杂度为O(N)。

桶内排序（线性时间复杂度）：对每个非空的桶进行排序的时间复杂度取决于桶内元素的个数和所使用的排序算法。如果桶内元素个数较少，可以使用简单且具有线性时间复杂度的排序算法（如插入排序）。因此，桶内排序的时间复杂度可以视为O(1)。

桶之间的合并（线性时间复杂度）：将各个桶中的元素按照顺序合并起来的时间复杂度为O(K)。

综上所述，桶排序的时间复杂度为O(N + K)，其中N是元素的数量，K是桶的数量。需要注意的是，当K接近N时，桶排序的时间复杂度接近O(N)，因此，桶的数量的选择对于桶排序的性能具有一定的影响。通常情况下，选择一个合适的桶的数量可以使得桶排序具有较好的性能。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int buckets[20001] = {0};
        for (int i = 0; i < nums.size(); i++) {
            buckets[nums[i] + 10000]++; //记录有几个大值
        }
        for (int i = 20000; i >= 0; i--) {
            k = k - buckets[i];
            if (k <= 0) {
            return i - 10000;
            }
        }
        return 0;
    }
};

查看评论

Leetcode个人笔记-medium

动态规划

121. 买卖股票的最佳时机

贪心

动态规划

1997. 访问完所有房间的第一天

前缀和优化

取mod技巧

70. 爬楼梯

拓展

0-1背包

代码模版

遍历方向如何判断？

完全背包

多重背包

递归

数组

704.二分查找

209.长度最小的子数组

54.遍历螺旋矩阵

59. 螺旋矩阵 II

前缀和

560. 和为 K 的子数组

链表

203.移除元素

19.删除链表的倒数第N个节点

142.环形链表II

哈希表

242.有效的字母异位词

1. 两数之和

15. 三数之和

字符串

344.反转字符串

541. 反转字符串II

151.翻转字符串里的单词

28.实现strStr()

KMP算法

459.判断重复字符子串

等价转化思维。证明用到string位置间的相等转化

双指针

栈与队列

队列：先进先出

232. 用栈实现队列

225. 用队列实现栈

20. 有效的括号

单调栈

739. 每日温度

496.下一个更大元素 I

503.下一个更大元素II

42. 接雨水

单调栈

双指针

84. 柱状图中最大的矩形

双指针

单调栈

哨兵

堆

215. 数组中的第K个最大元素

堆解法

桶排序解法