数据结构-树-学习笔记
部分树算法学习
Lecture 4 Tree
1. Tree 树
- 定义: A tree T is a collection of nodes(element). 树T是结点的集合
- The collection can be empty; otherwise, a tree consists of a distinguished node r, called the root, and zero or more nonempty(sub)trees T1, T2, ……, Tk(这个集合可能为空,否则这个树是由一个特殊的根节点和0个或多个子树组成)
1.1. 树的一些定义
- Degree of an elements(node) 节点的度数:有多少个子节点
- Degree of a tree 树的度:树里面结点的最大的度数。
- Leaf 叶节点:树里面度数为0的节点。
- Branch 分支节点:树里面度数不为0的节点。
- Level 层:根节点的层次为0或1,节点的层次等于其父结点的层次+1
- 树的高度:所有节点的最大层次数。
2. 二叉树
- 二叉树的定义:A binary tree t is a finite (possibly empty) collection of elements.(二叉树 t 是一个有限的节点的集合)
- 二叉树的特点:
- 二叉树的每个结点的度数为2
- 如果有子树,则子树均为二叉树,并且被称为左子树和右子树。
- 二叉树的左右子树是有区别的
2.1. 二叉树的应用
- 运算式的计算:转化成语法树后自带括号(运算次序)
2.2. 二叉树的性质(考前重点)
- n个结点的二叉树之间有n-1条边edges。
- 第i层的节点数最多是2^i个
- 高度为h(从0开始计)的二叉树中结点最少h+1个,最多2^(h+1)-1
- 如果一颗二叉树有n0个树叶,并且结点度数为2的节点有n2个,则n0=n2+1个
- 证明:设度数为1的节点为n1,则n=n0+n1+n2
- n = B + 1,B为边数(总节点数 = 边数 + 1)
- B = 1 * n1+ 2 * n2
- 不会证明用数学归纳法
- 有n个结点的二叉树的高度最大为n-1,最小为log2(n+1)(向上取整)-1(对应定理3)
2.3. 满full二叉树
- 将二叉树排满,也就是如果高度为n的树,其节点数为2n+1-1个
2.3.1. 完全complete二叉树
定义:Suppose we number the elements in a full binary tree of height h using the number 1 through 2h+1(假设我们为一个高度为h的满二叉树进行使用1 - 2^h+1的数字进行编码)
We began at level 0 and go down to level h.Within levels the elements are numbered left to right. (我们从0层到h层,从左向右进行编码)
从上到下,从左到右进行编码
性质六: Let i, 0 <= i <= n-1,be the number assigned to an element of a complete binary tree. The following are true.(假设i,0<=i<=n-1,是一个确定二叉树的一个节点的编号)(手画一个试试就好)
- if i=0, then this element is the root of the binary tree. if i>0,then the parent of this element has been assigned the number (i-1)/2(向下取整)(如果i=0,则是根节点,不然其父结点的编号为 (i-1)/2(向下取整))
- if 2*i+1 >= n,then this element has no left child. Otherwise,its left child has been assigned the number 2*i+1.(如果2*i+1>=n,那么这个元素没有左子女,不然左子女的编号就是这个数字)
- if 2i+2>=n, then this element has no right child, Otherwise its right child has been assigned the number *2i+2*.(如果2*i+2>=n,那么这个元素没有右子女,不然右子女的编号就是这个数字)
完全二叉树和满二叉树是不同的,完全二叉树的最后一层可以不全满,但是必须从左开始顺序无空缺。
2.4. 物理实现二叉树
2.4.1. 数组实现二叉树
- 其标记为其在数组中的下标,使用数组来存储。
- 常规二叉树的数组表示的位置上一定有空的。
- 很稀疏的二叉树会导致数组存储二叉树有大量的内存空间被浪费掉。
2.4.2. 链表实现二叉树
- Linked representation( also called L-R linked storage) 也被称为L-R链表存储。
- 二叉树节点
1 | |
- 二叉树
1 | |
- 正常二叉树操作
- In this class ,we employ a linked representation for binary trees.在这个class中我们使用链表来代表二叉树
- The function visit is used as parameter to the traversal methods,so that different operations can be implemented easily 函数visit被用作遍历方法的一个参数所以我们可以实现不同的操作更加简单
2.4.3. 链表具体实现方法细节
- 补充C++知识:
- Class::f()实现Class中的f()方法
1 | |
- 二叉树的应用
1 | |
2.5. 二叉树遍历
- 以下算法中的二叉树是通过链表实现的。
- Each element is visited exactly once
- V—–表示访问一个结点 vertice
- L—–表示访问V的左子树 left tree
- R—–表示访问V的右子树 right tree
- 所有的遍历顺序:VLR\LVR、LRV、VRL、RVL、RLV
- 常用的遍历顺序
- 先序遍历:VLR
- 中序遍历:LVR
- 后序遍历:LRV
- 广度优先遍历:先处理树根节点,然后处理靠近的第一层的节点
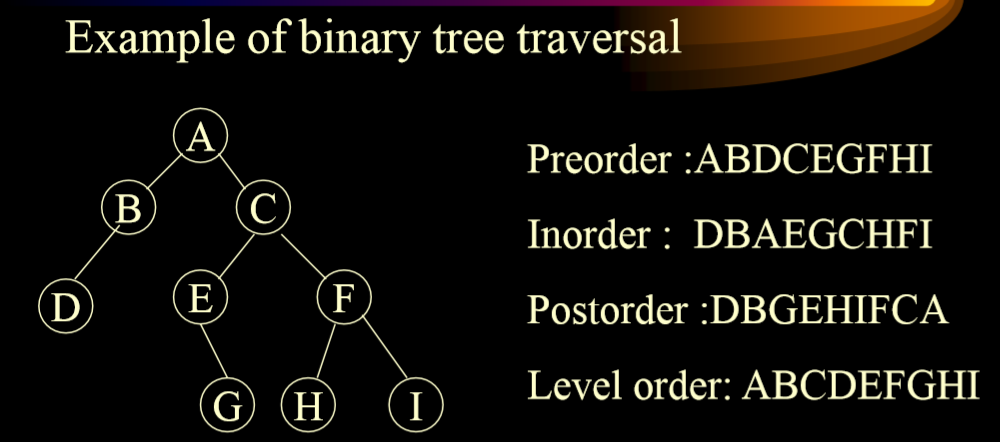
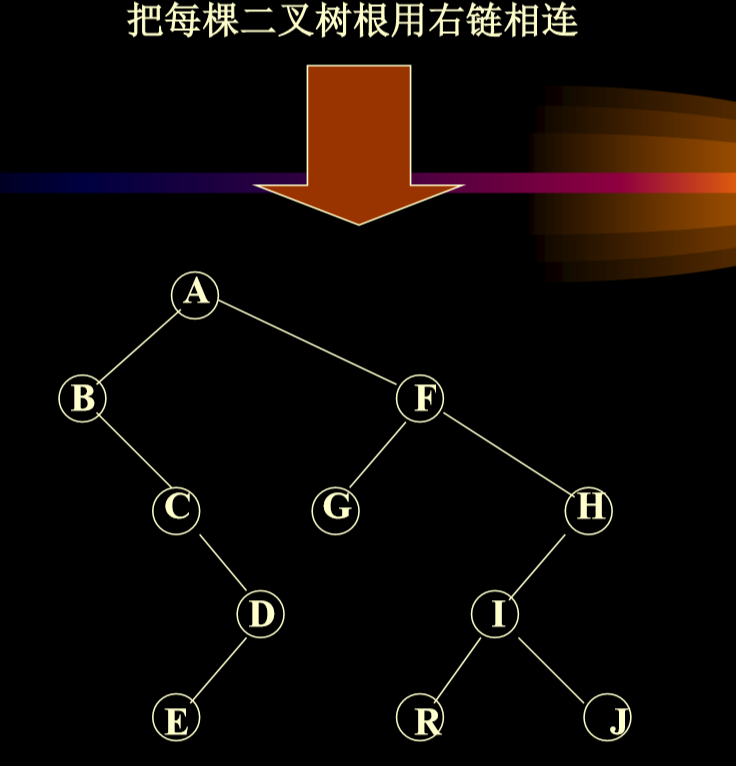
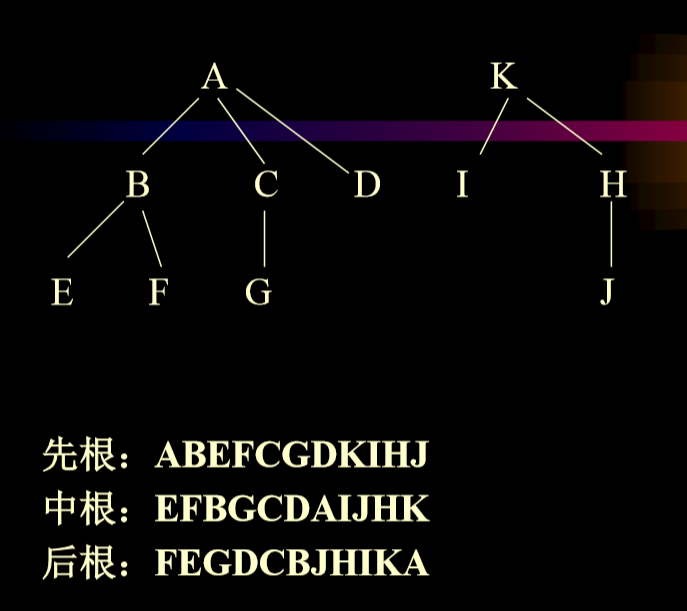
2.5.1. 例子
2.5.2. 先序遍历
- VLR
1 | |
2.5.3. 中序遍历
1 | |
2.5.4. 后序遍历
1 | |
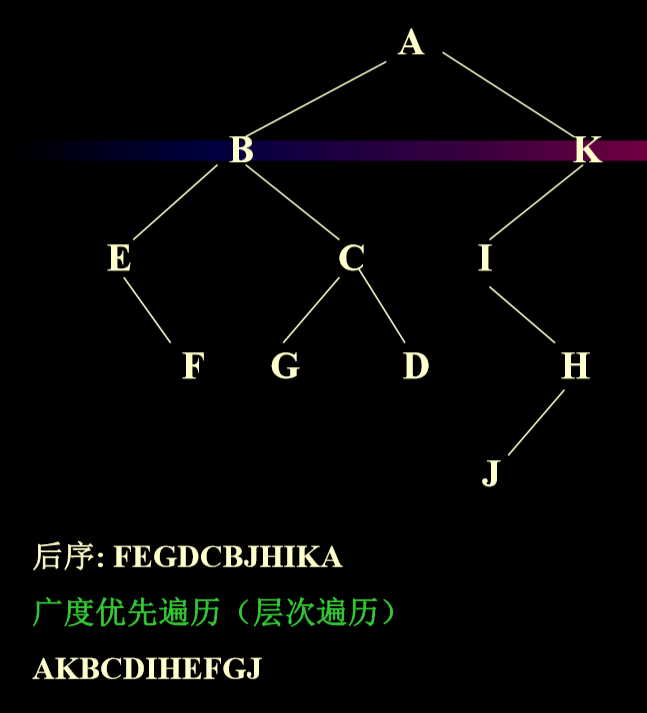
2.5.5. 广度优先遍历
- 根据level order(树的层数)
数组实现
- 直接按顺序访问数组即可
链表实现
1 | |
2.6. 建立二叉树
2.6.1. 利用MakeTree函数
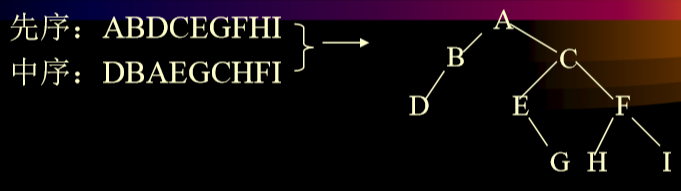
2.6.2. 利用先序、中序唯一的构造一颗二叉树
2.6.3. 利用二叉树的中序、后序遍历确定一颗二叉树
后序的最后是根节点,根据中序进行划分
2.6.4. 利用二叉树的广义表来构造一颗二叉树
2.6.5. 利用二叉树的后缀表示来构造一颗二叉树
2.6.6. 利用二叉树的后缀表示来构造一颗二叉树
3. 精讲:利用先序、中序唯一的构造一颗二叉树(string)
- 字符串(简称串)的定义以及一些术语
- 串:是n(n>=0)个字符的一个有限序列,开头结尾用双引号””括起来。
- 串的长度:串中所包含的字符个数n(不包括分界符‘ “ ’,也不包括串的结束符‘\0’)
- 空串:长度为0的串。或者说只包含串结束符‘\0’的串,空串不等同于空白串。
- 子串:串中任一连续子序列
3.1. 其他的二叉树的方法
- PreOutput():output the data fields in preorder
- InOutput():output the data fields in inorder
- PostOutput():output the data fields in postorder
- LevelOutput():output the data fields in level order
- Delete():delete a binary tree,freeing up its nodes
- Height():return the tree height
- Size():return the number of nodes in the tree
- The height of the tree is determined as: max{hl, hr}+1
1 | |
3.2. String
1 | |
3.3. String部分方法的实现
1 | |
3.4. 根据先序遍历和中序遍历生成二叉树的思路
- 先序遍历的第一个一定是树根,然后在中序遍历中找树根,然后在中序中树根左边是左子树,右边是右子树
3.5. C++实现
1 | |
3.6. 已知其他的遍历顺序来生成二叉树
3.6.1. 已知后序遍历和中序遍历
- 先序遍历的树根在头部,而后序遍历串的树根在尾部。
3.6.2. 已知先序遍历和后续遍历串
- 先序遍历串的第二个位置是左子树(左右子树分界点),然后我们和后序遍历串结合。
3.7. 二叉树的应用
3.7.1. 二叉树的表示方式
- Binary-Tree Representation of a Tree 树的存储方式:三种
- 广义表表示:a(b(f,g),c,d(h,i,j),e)
- 双亲表示法;记下自己的父结点位置,问题是:找子节点需要遍历一遍。
- 左子女—右兄弟表示法
!(img/cpt5/4.png)
1 | |
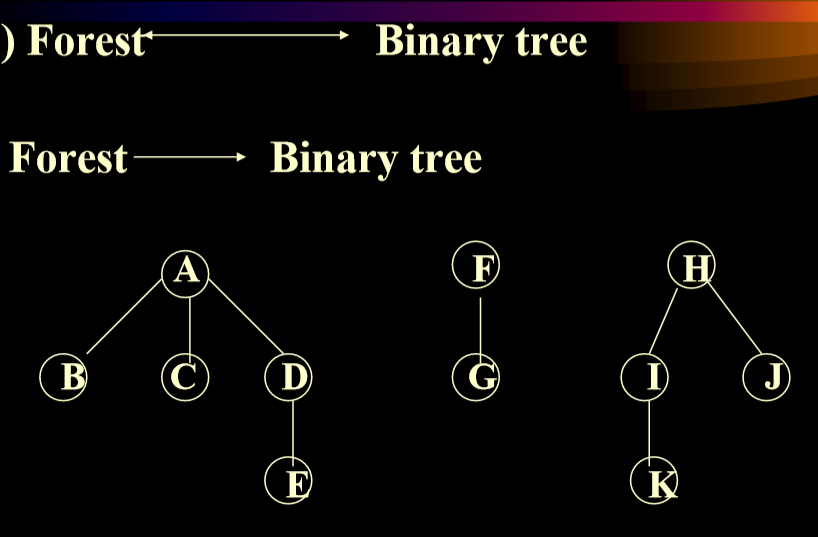
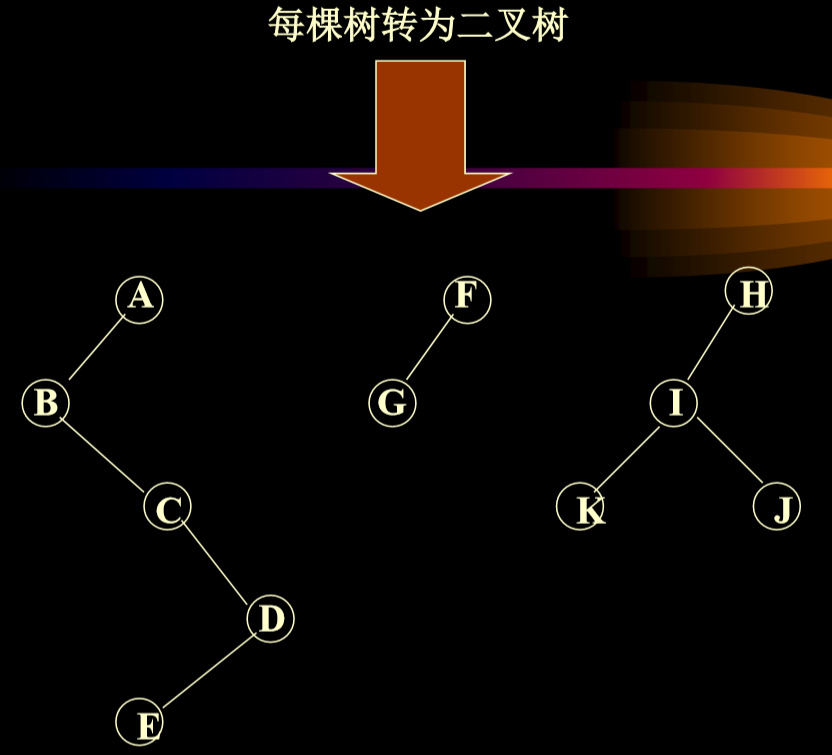
3.7.2. 将森林转换成二叉树
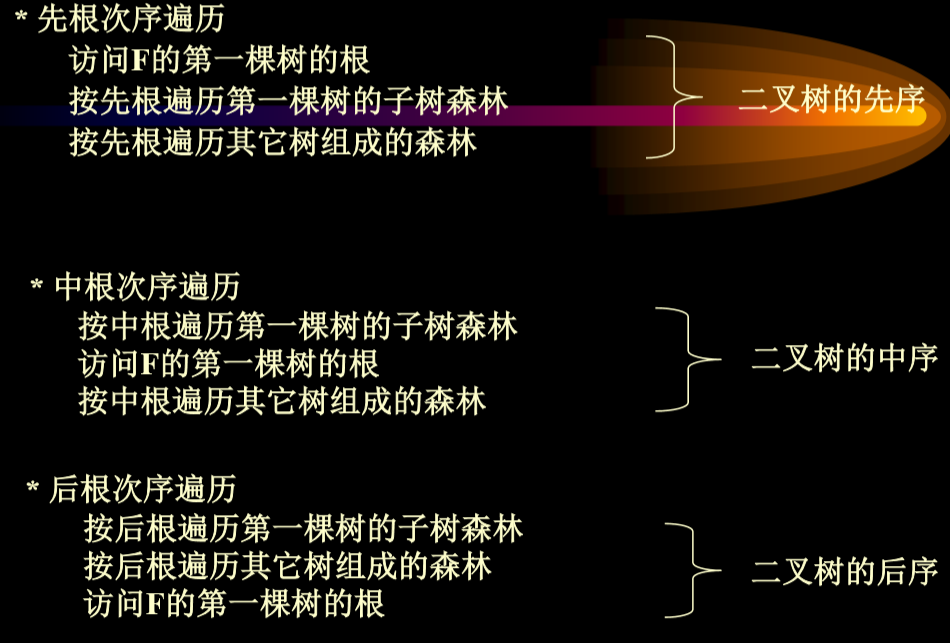
3.8. 树的遍历
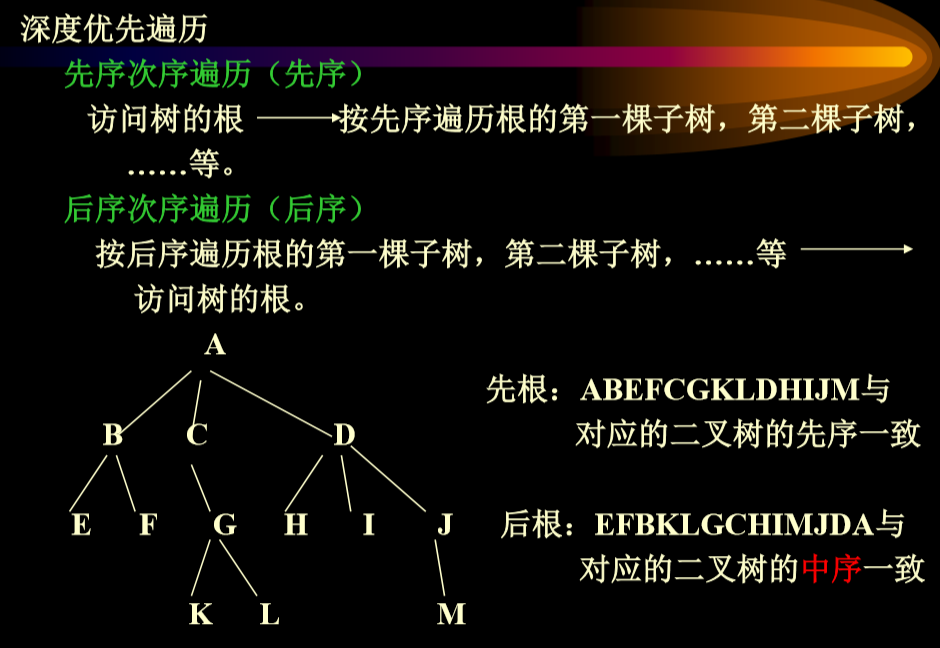
3.8.1. 深度优先遍历(DFS)
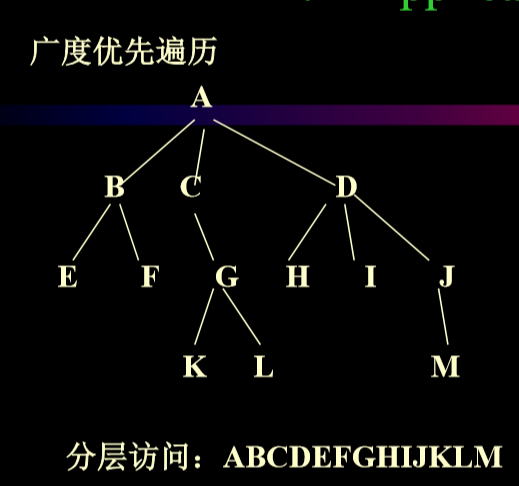
3.8.2. 广度优先遍历
3.9. 森林的遍历
- 应用左子女-右兄弟的二叉树进行遍历
3.9.1. 深度优先遍历
- Eg.
- 生成左子女-右兄弟二叉树后正常遍历即可
4. 线索二叉树
- 目的:让二叉树遍历的速度更快
- 特点:在树的节点中加入一个指针(比如指向下一个节点)
- n个结点的二叉树有2n个链域,其中真正有用的是n–1个,其它n+1个都是空域(null)。为了充分利用结点中的空域,使得对某些运算更快,如前驱或后继等运算。
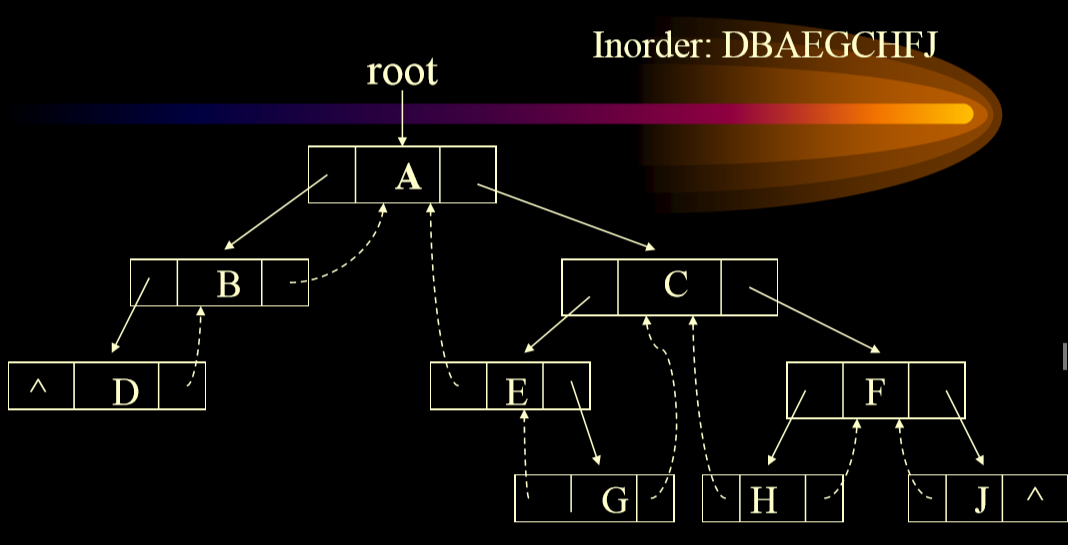
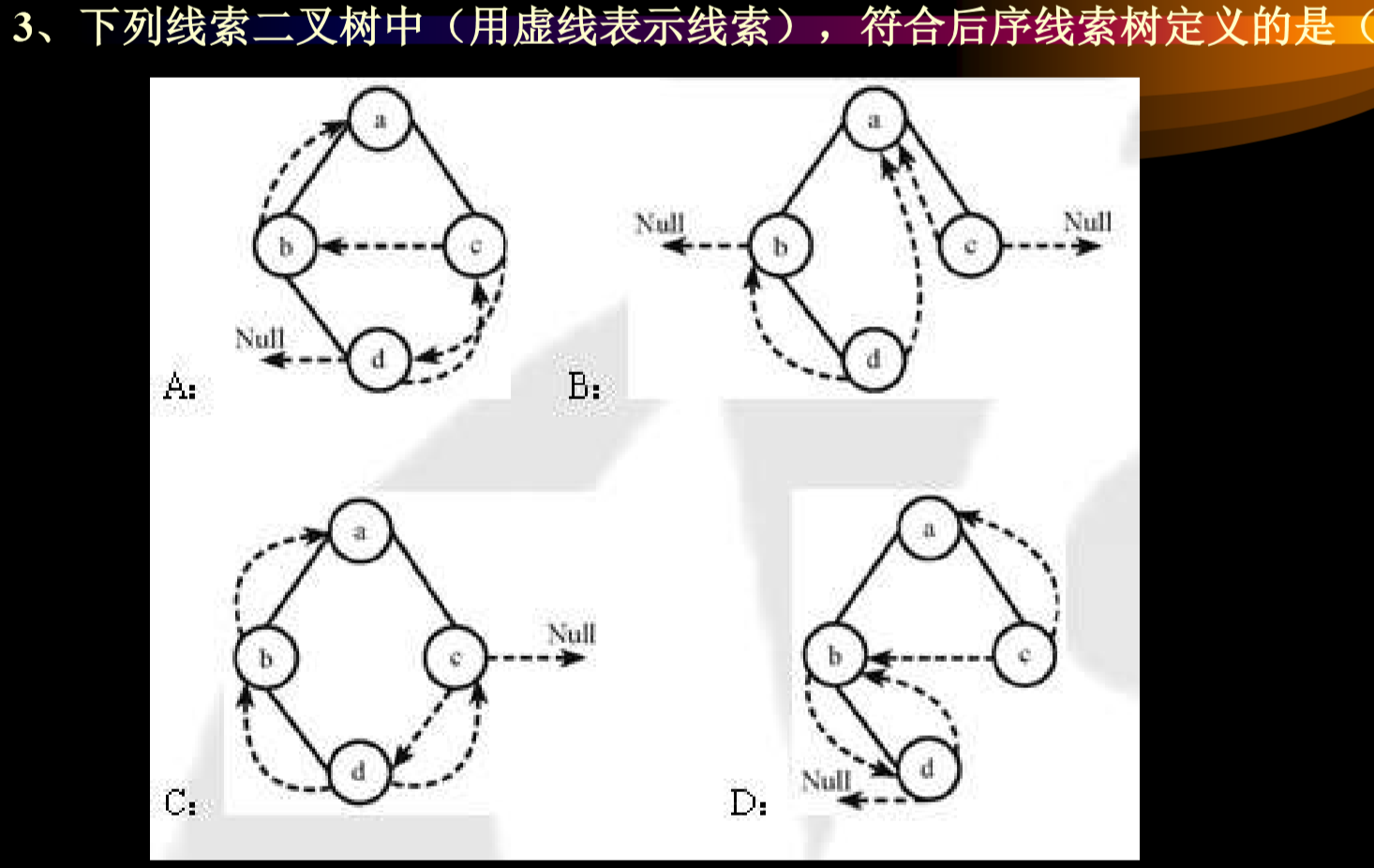
4.1. 例子
- 虚线是本身被置为NULL的部分
- 使用左指针指向中序遍历前项,使用右指针指向中序遍历的后项。
- 唯二空指针:最左边节点的左指针,最右边节点的右指针
- 整个树只会有两个空指针
4.2. 线索二叉树的结点的数据结构
4.3. 线索二叉树类的实现
1 | |
4.4. 中序遍历已有的中序线索二叉树
- 按中序遍历中序线索树
- 遍历算法(以中序为例):
- 递归, 非递归(需用工作栈)
- 这里前提是中序线索树, 所以既不要递归, 也不要栈。
- 遍历算法:
- 找到中序下的第一个结点(first)
- 不断找后继(Next)
- 如何找后继?
- 遍历算法(以中序为例):
- 情况一:如果p结点没有右子树(p->rightthread == 1)则 p=p->rightchild(右链就是后继)
- p有右子树(p->rightThread==0) 则
- p=p->rightchild
- while(p->leftThread==0) p=p->leftchild;
1 | |
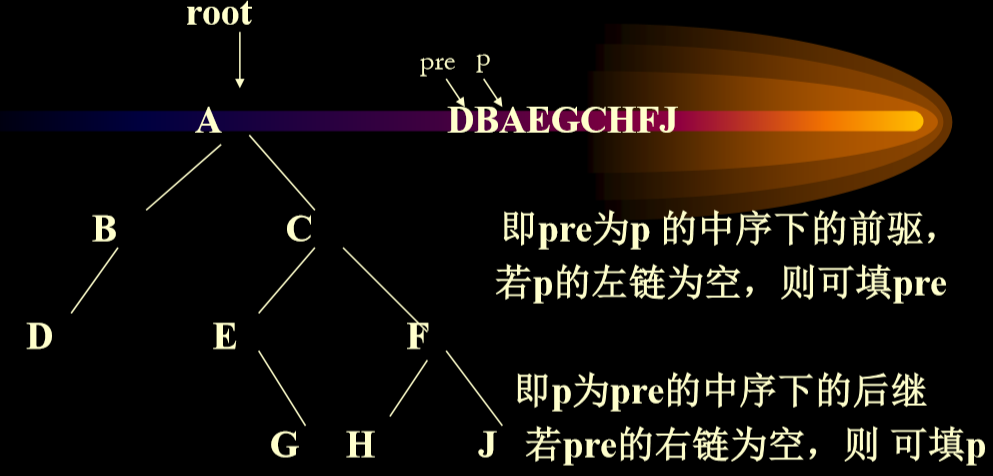
4.5. 建立中序线索二叉树
- 对已存在的一棵二叉树建立中序线索树
- 分析:与中序遍历算法差不多,但是要填左空域,右空域的前驱、后继指针。所以除了流动指针p外,还要加一个pre指针,它总是指向遍历指针p的中序下的前驱结点。
- pre相当于记录下来整个遍历顺序来完成链接
- Eg.
1 | |
5. 树的应用
5.1. 哈夫曼树(Huffman Tree)
5.1.1. 一些概念
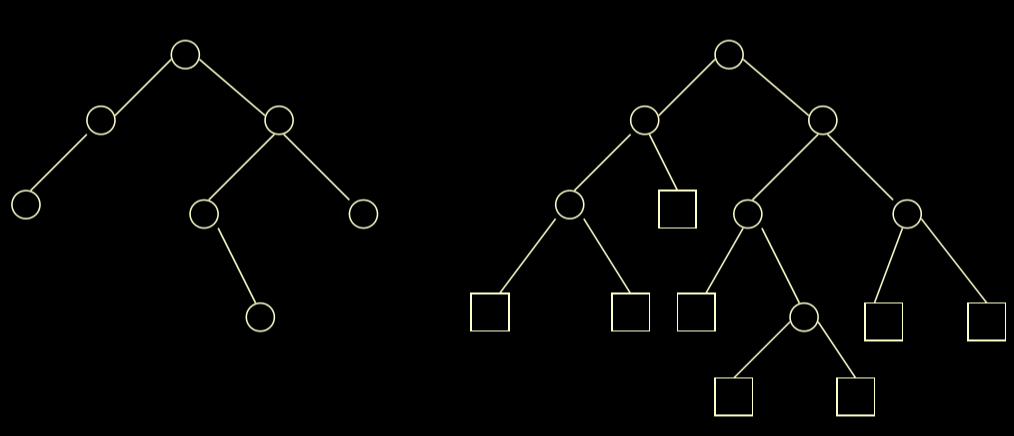
增长树(使得原来的树的每一个度数都为2)
- 对原二叉树中度为1的结点,增加一个空树叶
- 对原二叉树中的树叶,增加两个空树叶
外通路长度(外路径)E
根到每个外结点
(增长树的叶子)的路径长度的总和(边数)
- E = 3+3+2+3+4+4+3+3=25,如右上图例
内通路长度(内路径)I:
根到每个内结点
(非叶子)的路径长度的总和(边数)。原来的树上每一个节点到树根的长度的综合
- I=2+1+0+3+2+2+1=11 如右上图例
结点的带权路径长度:一个结点的权值与结点的路径长度的乘积。
- 每个结点的权重占有一定的值
带权的外路径长度:各叶结点的带权路径长度之和。
带权的内路径长度:各非叶结点的带权路径长度之和。
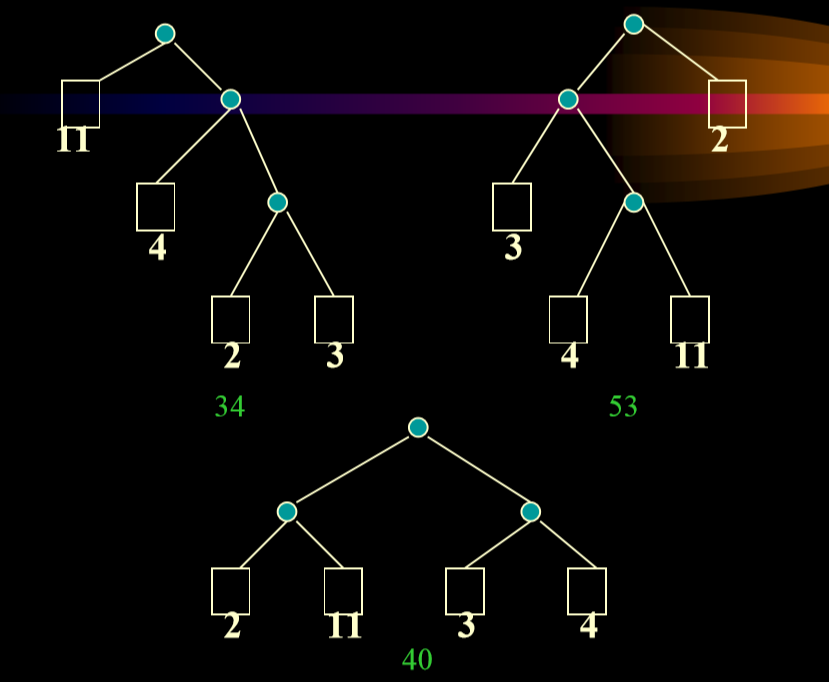
例子如下
- 从形状上来讲,二叉树有以上三种大致形状。
5.1.2. Huffman算法
- 思想:权大的外结点靠近根,权小的远离根。
- 算法:从m个权值中找出两个最小值W1,W2构成
- 就是把计算结果放进去和其他节点一起选出两个,进行迭代
- 所以我们就是把数字比较大的挂到距离根比较近的地方
- 内节点不会只有一个叶节点。
5.1.3. 霍夫曼编码
- 是霍夫曼树在数据编码中一种应用。具体的讲用于通信的二进制编码中。设一电文出现的字符为D={M,S,T,A,Q, K},每个字符出现的频率为W={10,29,4,8,15,7},如何对上面的诸字符进行二进制编码,使得
- 该电文的总长度最短。
- 为了译码,任一字符的编码不应是另一字符的编码的前缀
- 根据树情况,我们知道编码是不具有二义性的,必然唯一对应,一个叶节点就一个结果
6. 考研例题
6.1. 2019年
- D
- 4题:C 第七层48+前六层63(第六层:8个叶节点+24个根节点)
- 5题:B 左子女右兄弟,枚举法,v有四种情况,按照左子女右兄弟即可
- 最左边:不是父子也不是兄弟关系
- 第二个:父子
- 第三个:无关系
- 第四个:兄弟
6.2. 2020年
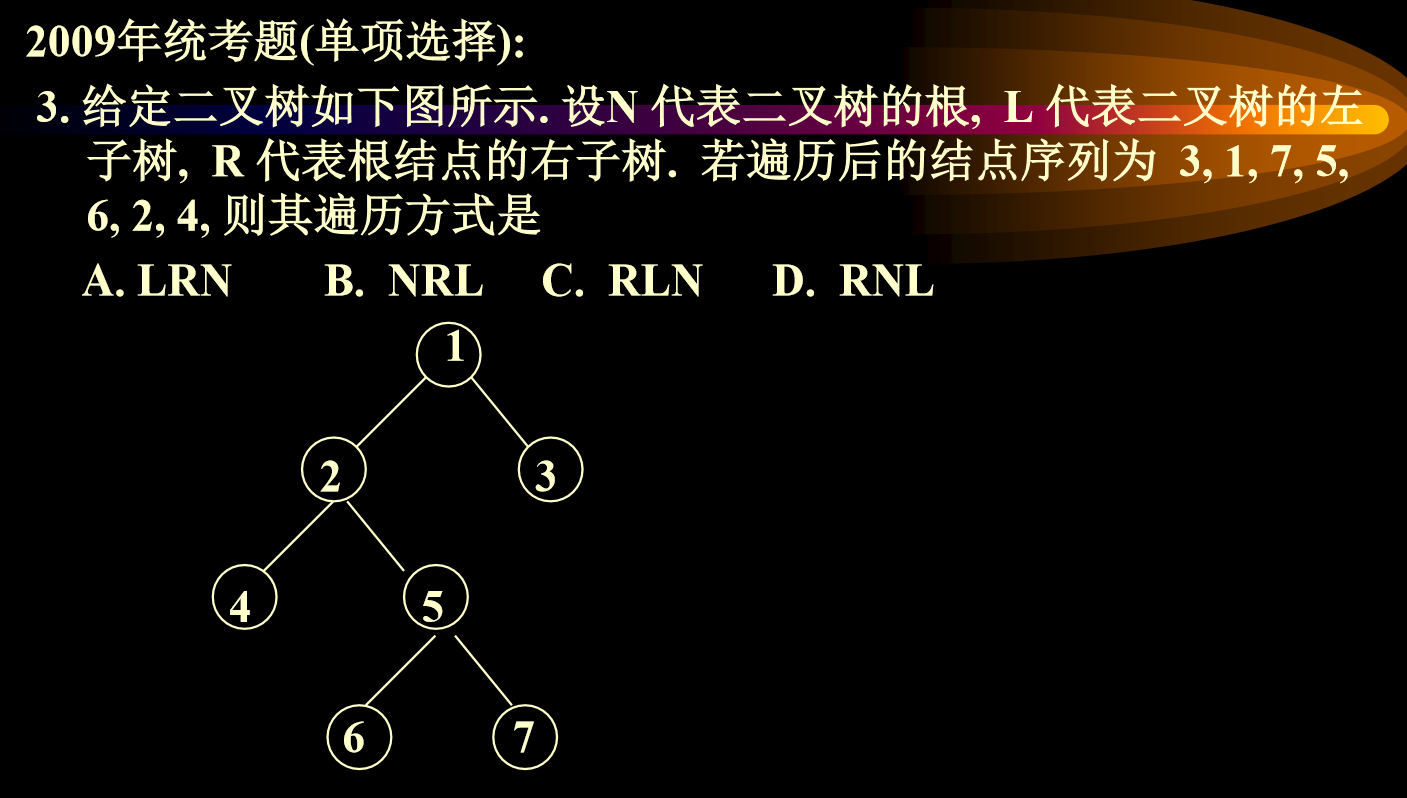
- 3题:D
- 5题:B
- 总结点数:(20*4+10*3+1*2+10*1+1)-(20+10+1+10)=82 所有节点-有子节点
- 6题:A
- 根节点度数可以为1,树中不含树根
7. 广义表
7.1. 广义表定义
- 定义为n(n>=0)个表元素a0,a1,a2,……an-1组成的有限序列, 记作: LS=(a0,a1,a2,……an-1)
- 其中每个表元素ai可以是原子,也可以是子表.
- 原子: 某种类型的对象,在结构上不可分(用小写字母表示).
- 子表: 有结构的。(用大写字母表示)
- Eg.L = (3,(),(b,c),(((d))))
7.2. 广义表基础概念
- 长度:表中元素的个数
- 广义表的表头,表尾
- head= a0;
- tail= (a1, a2,……an-1)
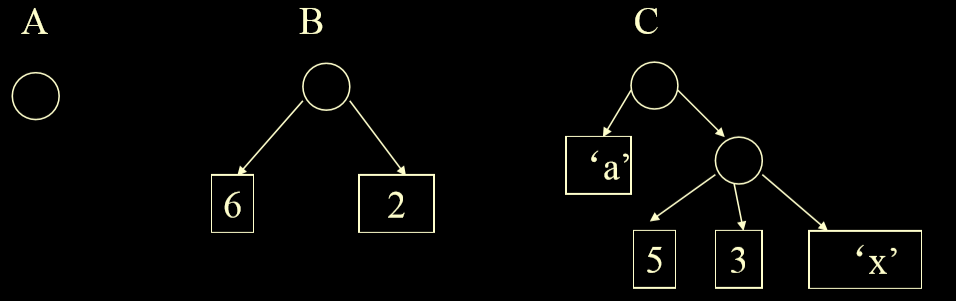
- C=(a,(5,3,x)) 表头为a,表尾为((5,3,x))
- 广义表的深度:表中所含括号的最大层数
7.3. 广义表的性质
- 有序性
- 有长度,有深度
- 可递归,如上面例6
- 可共享,如E中B为E,D所共享
- 各种广义表都可用一种示意图来表示,用圆表示表元素, 用长方形表示原子
7.4. 广义表的操作
7.5. 广义表的实现
7.6. 广义表的类声明
1 | |
7.7. 广义表的实现
7.7.1. 求解广义表深度
1 | |
7.7.2. 判断两个广义表的相等关系
- 相等的条件: 具有相同的结构,对应的数据元素具有相等的值
1 | |
7.7.3. 广义表的复制算法
- 分别复制表头,表尾,然后合成,前提是广义表不可以是共享表或递归表
1 | |
7.7.4. 广义表析构函数
1 | |
Lecture 4.5 特殊树
1. 二叉搜索树
- Definition: A binary search tree is a binary tree that may be empty. A nonempty binary search tree satisfies the following properties:(二叉搜索树是一个可以为空的二叉树。一个非空的二叉树都满足如下性质)
- Every element has a key and no two elements have the same key; therefore,all keys are distinct. (每一个元素都含有一个关键字,并且每一个元素都有独一无二的关键字)
- The keys(if any)in the left subtree of the root are smaller than the key in the root.(一个树的左子树的关键字小于根中的关键字)
- The keys(if any)in the right subtree of the root are larger than the key in the root.(一个树的右子树的关键字大于根中的关键字)
- The left and right subtrees of the root are also binary search trees.(根的左右子树还是二叉搜索树)
- 二叉搜索树需要满足的事情:在很大的数据量下,要能够
1 | |
1.1.2. 二叉搜索树需要实现的方法
1 | |
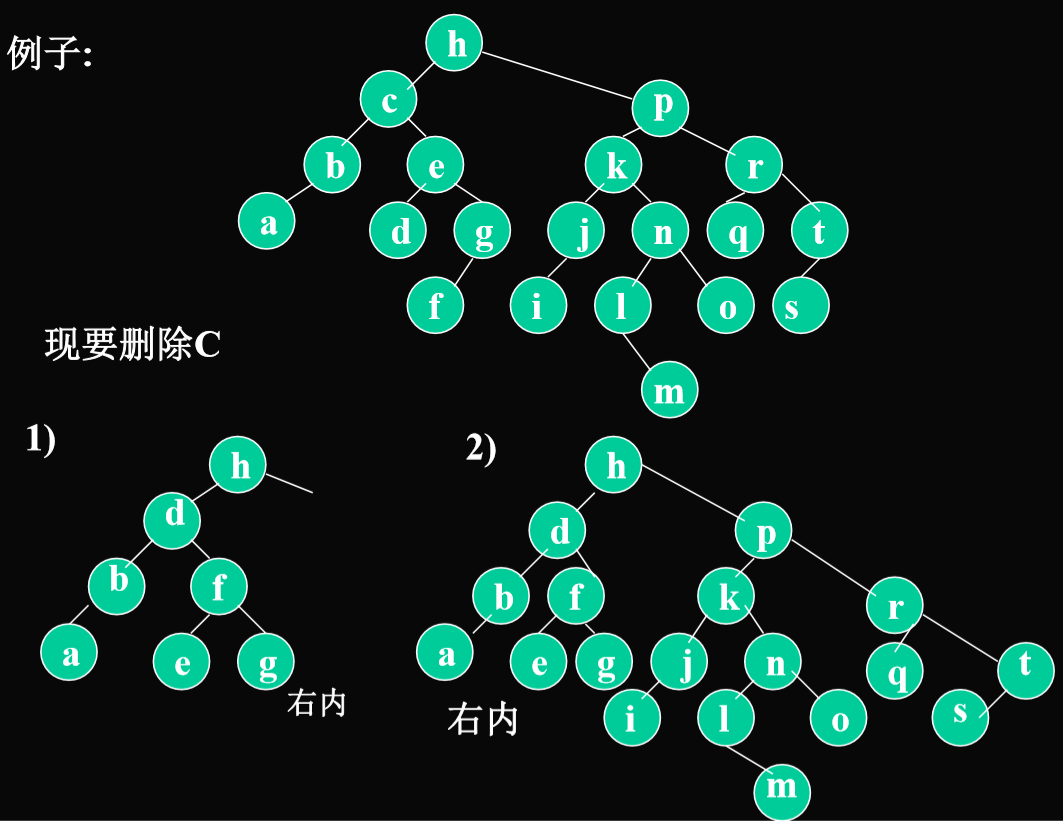
删除算法
- 如果结点本身不在树内,那么不需要删除
- 如果结点本身在树里面,删除需要分类
- 无子树:删除叶节点
- 一颗子树:直接连接
- 两颗子树:可以选择左子树的最大结点作为新结点
1 | |
高度
- The height of a binary search tree has influence directly on the time complexity of operations like searching, insertion and deletion. 二叉搜索树的高度会影响搜索,插入和删除算法的搜索度
- Worst case: add an ordered elements{1,2,3…n} into an empty binary search tree. 最坏的情况就是把一个有序的数列添加进入到空的二叉搜索树中去。
二叉搜索树的算法复杂度
- 二叉搜索树以上的所有操作都和二叉搜索树的深度有关,所以在生成二叉树的时候我们需要保证二叉搜索树的平衡性,(如果一开始输入最小的,树严重失衡,如果一开始输入中等,树基本平衡)
- Best Case:O(log2n)
1.2. 索引二叉树
- An indexed binary search tree is derived from an ordinary binary search tree by adding the field leftSize to each tree node. 索引二叉搜索树是通过将字段leftSize添加到每个树节点,从普通二叉搜索树派生而来的。
- Value in Leftsize field=number of the elements in the node’s left subtree +1(leftsize = 左子树大小 + 1)
- Eg.
2. AVL Tree(自平衡的二叉搜索树)
- 目的:the AVL tree was introduced to increase the efficiency of searching a binary search tree, and to decrease the average search length. AVL树是一个用来增加二叉搜索树的平衡性并且减小平均搜索高度
- AVL的高度是O(log2 n)的,所以对应的算法复杂度也是这样的。
2.1. 什么是AVL树
- AVL树是一个二叉搜索树
- AVL树的每一个节点满足|hL-hR|<=1 where hL and hR are the heights of TL(left subtree) and TR(right subtree),respectively.对于每一个结点,其左子树和右子树的高度之差不超过1
- 注:树叶之间之差未必小于一,但是一个节点的左右子树的高度不能大于一
2.2. AVL树的基本概念
- AVL树高:the longest path from the root to each leaf node(从根节点到每一个叶节点之间的所有路径的最长的一条)
- Balance factor bf(x) of a node x : height of right subtree of x – height of left subtree of x 节点x的平衡因子 = x的右树的高度-x的左树的高度
2.3. AVL树的结点的实现
2.4. AVL树的实现
- 这个例子里每个结点中存储着树高
- 树高之差就是平衡因子
1 | |
2.5. AVL树的基本操作
2.5.1. AVL树的查询
查询过程和正常的二叉搜索树是相同的,其算法复杂度和正常二叉搜索树的搜索算法的复杂度是相同的。
2.5.2. AVL树的插入
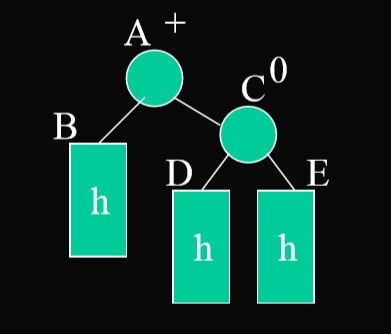
- 简单来看,每一个子树都可以被看为如上的图
- 算法流程:是递归从下向上进行旋转处理,先看子树。
插入C的右子树E(外侧结点)
- 只需要进行一次左单旋转即可
- 左单旋转过程如上
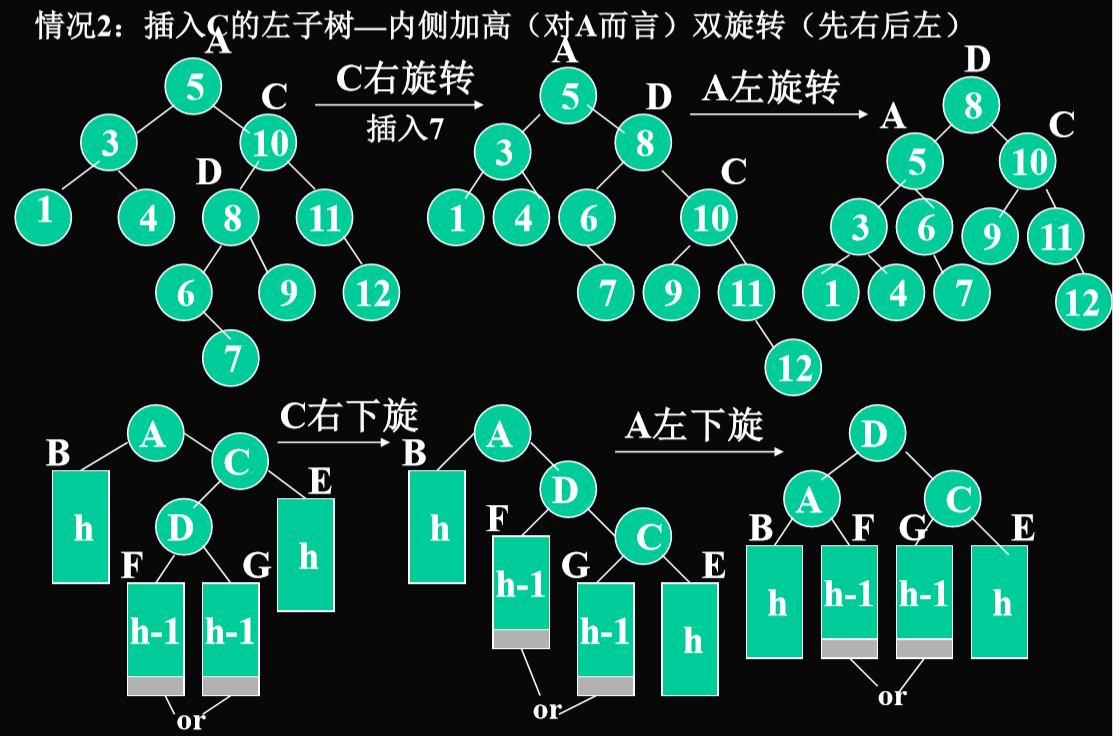
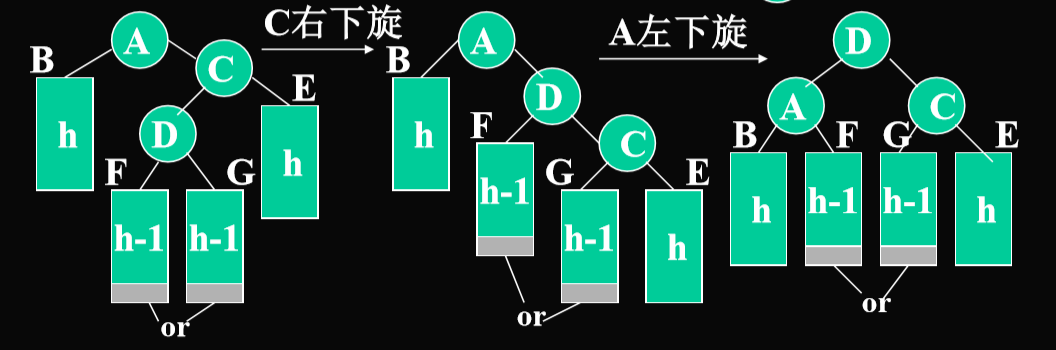
插入C的左子树D(内侧结点)
- 需要进行一次双旋转(先右后左)
插入其他地方,树不需要转
- 一直到5的时候,树的平衡性才受到影响
- 插入后,树的平衡性没有被破坏显然不用旋转
- 调整只要在包含插入结点的最小不平衡子树中进行,即从到达插入结点的路径上,离插入结点最近的,并且平衡系数!=0的结点为根的子树.
算法思想与总结(考试可能画图)
- 算法思想:插入一个新结点后,需要从插入位置沿通向根的路径回溯,检查各结点左右子树的高度差,如果发现某点高度不平衡则停止回溯。
- 先确定节点是在外侧还是内侧,决定是单旋还是双旋
- 单旋转:外侧—从不平衡结点沿刚才回溯的路径取直接下两层如果三个结点处于一直线A,C,E
- 双旋转:内侧—从不平衡结点沿刚才回溯的路径取直接下两层如果三个结点处于一折线A,C,D
- 以上以右外侧,右内侧为例,左外侧,左内侧是对称的。与前面对称的情况:左外侧,左内侧 左外侧
- 插入:
- 首先要找到正确的位置进行插入
- 找到有可能发生不平衡的最小不平衡子树
- 判别插入在不平衡子树的外侧还是内侧
- 根据3的判别结果,再进行单旋还是双旋
例子(从空的AVL树建树的算法)
- 右双旋转:先变成ACZ,再把AC旋转下去。
- 左子树的左子树是左外侧,左子树的右子树是左外侧,右子树的左子树是右内侧,右子树的右子树是右外侧
- 判断内侧外侧只从被破坏根节点向下2层。
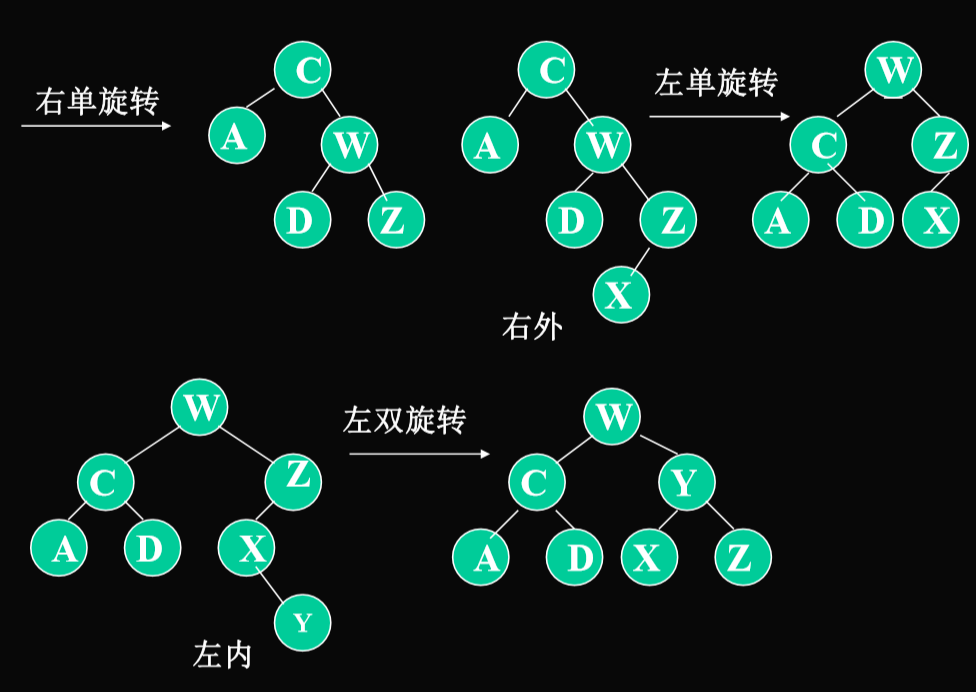 img
img
- 判断内侧外侧只从被破坏根节点向下2层。
插入算法代码
1 | |
右下旋
1 | |
左下旋
1 | |
右内侧
1 | |
左内侧
1 | |
2.5.3. AVL树的删除
- 方法和二叉搜索树的删除方法一样
- 需要找到被删除顶点的中序后继。
- 等待再看一下。
例子
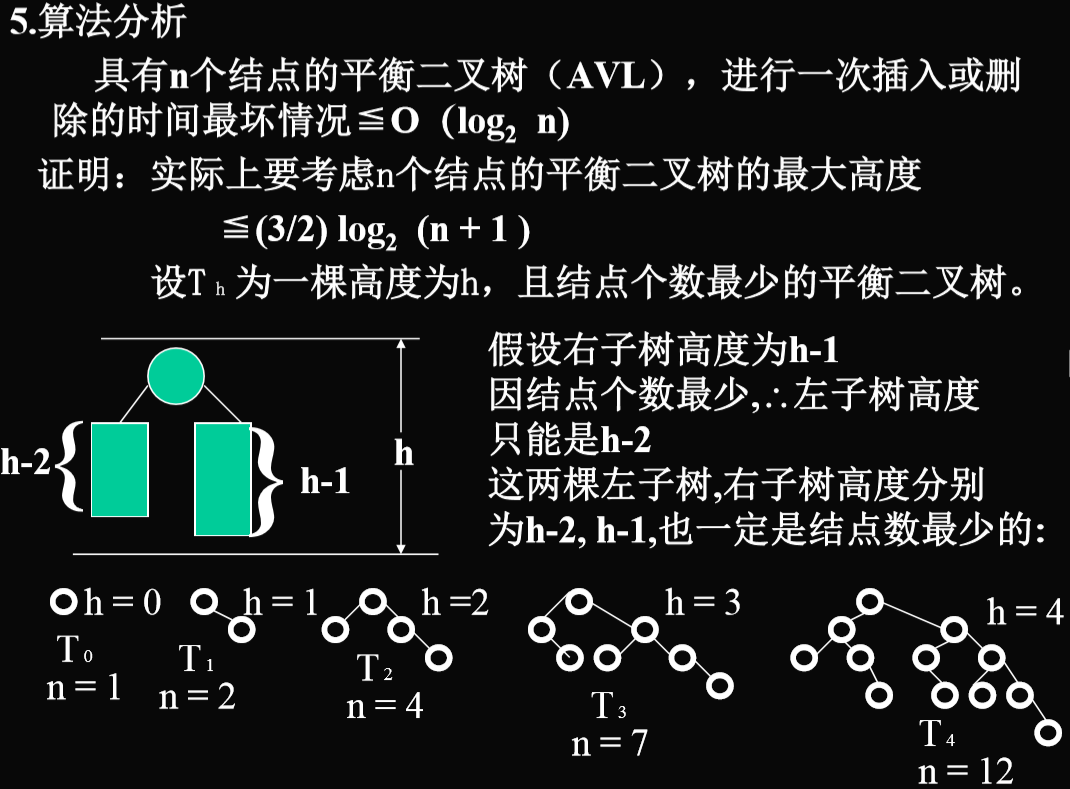
2.5.4. 算法复杂度分析(不做要求)
3. B-TREES
3.1. m叉搜索树
3.1.1. m叉搜索树的定义
Definition: An m-way search tree may be empty. If it is not empty, it is a tree that satisfies the following properties: m-way搜索树可能为空。如果是一个非空的树,则为满足以下属性的树:
- In the corresponding extended search tree(obtained by replacing zero pointer with external nodes), each internal node has up to m children and between 1 and m-1 elements.(在相应的扩展搜索树(用外部节点替换零指针获得)中,每个内部节点最多有m个子节点,在1和m-1元素之间。)
- Every node with p elements has exactly p+1 children.(每个具有p元素的节点正好有p+1子节点。)
- Consider any node with p elements:
 img k1 < k2 <……< kp, c0,c1,……,cp be the p+1 children of the node 假设任何节点都有p个元素,那么C0 - Cp是他们对应的p+1个子元素。
img k1 < k2 <……< kp, c0,c1,……,cp be the p+1 children of the node 假设任何节点都有p个元素,那么C0 - Cp是他们对应的p+1个子元素。
对于
 img
img中的节点:
- C0: The elements in the subtree with root c0 have keys smaller than k1(在以C0为根的所有子树中的结点的值都小于k1)
- Cp: Elements in the subtree with root cp have keys larger than kp(在以Cp为根的子树中的所有子树的值都大于Kp)
- Ci: Elements in the subtree with root ci have keys larger than ki but smaller than ki+1, 1<=i<=p.
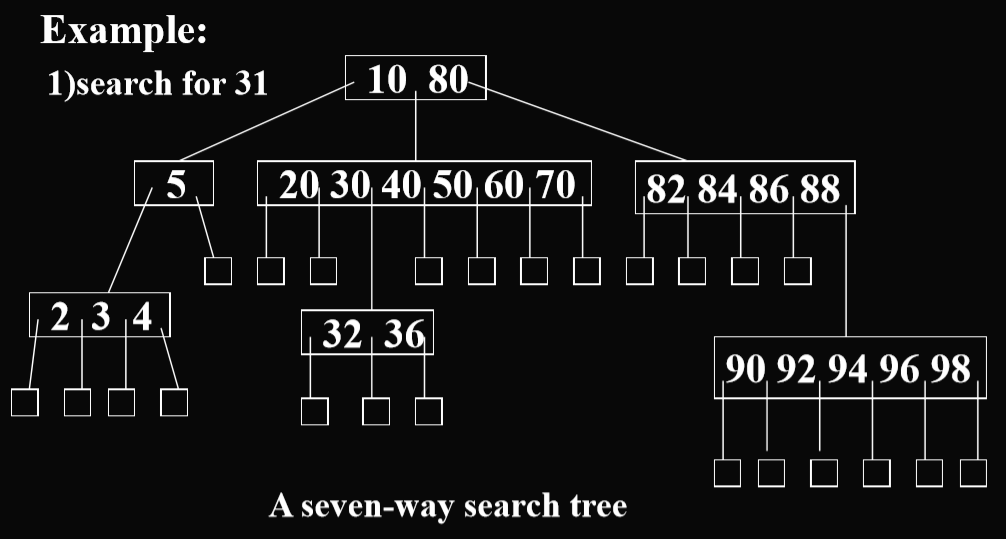
m叉搜索树的例子:
- m叉搜索树是可以存入磁盘的。
3.1.2. 操作
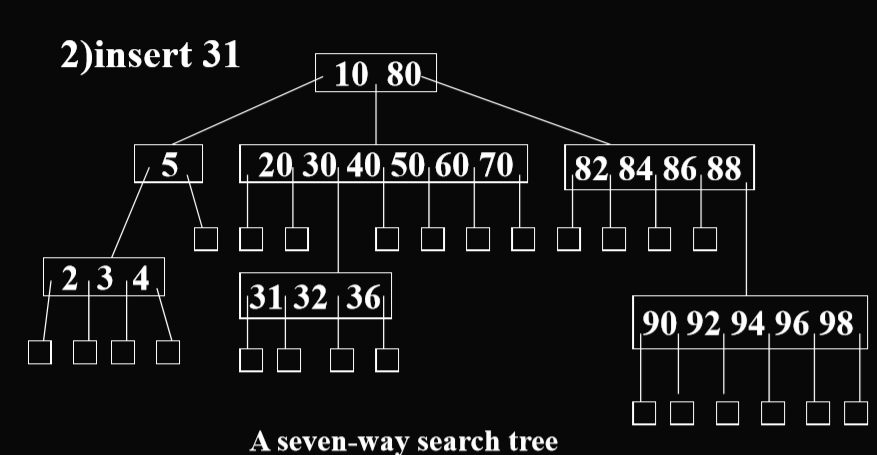
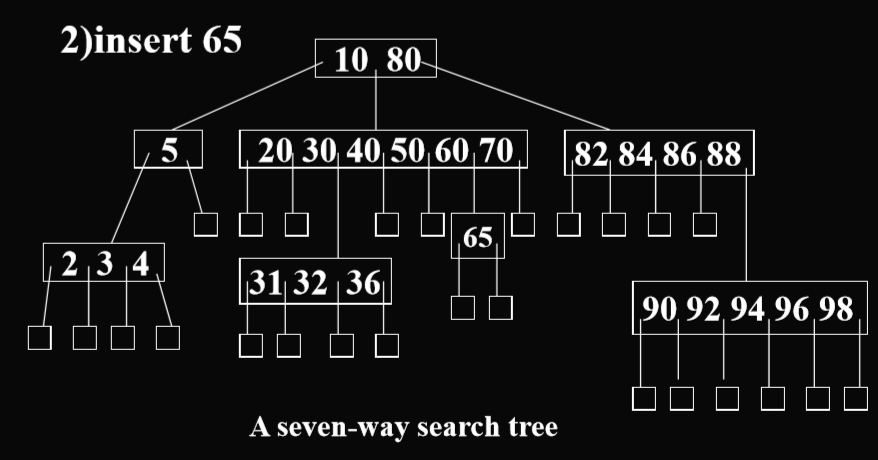
插入操作
- 如果一层没有满,就在同一级进行插入。(针对的是m叉的情况)
- 如果这一层已经满了,那么在下一层进行插入。
- 例子
- 注:n叉搜索树,每一层一个结点最多有n-1个元素
删除操作
查找m叉搜索树的行高
- Height of an m-way search tree(m叉二叉树的行高)
- An m-way search tree of height h may have as few as h elements(one node per level), as many as mh-1 elements.(一个高为h的m路搜索树最少有h个结点(每一层只有一个结点),最多有mh-1个结点)
- The height of a m-way search tree with n elements is between logm(n+1) and n
- n: 2005-1 =32*1010-1
3.2. 平衡的m路搜索树——B树
- Definition : A Btree of order m is an m-way search tree. If the Btree is not empty, the corresponding extended tree satisfies the following properties:m阶的B树是一个m叉搜索树。如果B树不为空,则B树有相应的扩展属性:
- the root has at least two children(每个根结点至少有两个子女)
- all internal nodes other than the root have at least m/2(向上取整) children(所有内节点都至少有m/2(向上取整)个子结点)
- all external nodes are at the same level(所有的外节点必须都在同一层)
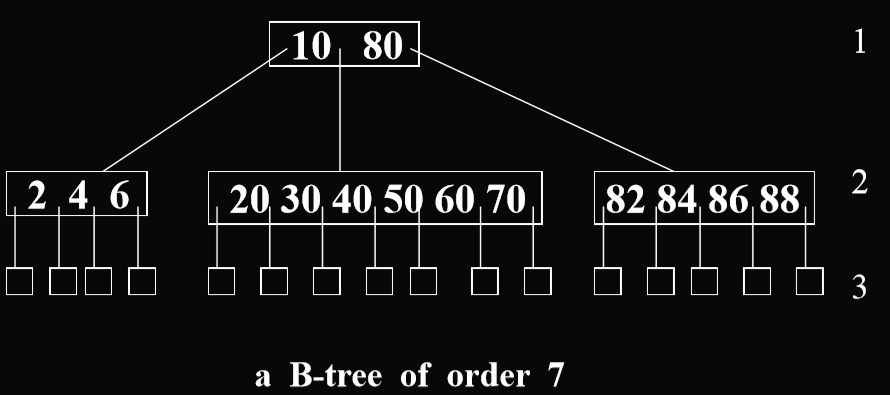
- Eg.
- 早一点的数据库用的是B树,现在大数据数据库是B+树。
- Eg1. In a Btree of order 2, each internal node has at least 2 children, and all external nodes must be on the same level, so a Btree of order 2 is full binary trees (在二阶B树中,每一个内部节点都有至少2个子女,并且所有的外部节点都必须在同一级上,所以2阶B树是满阶二叉树)
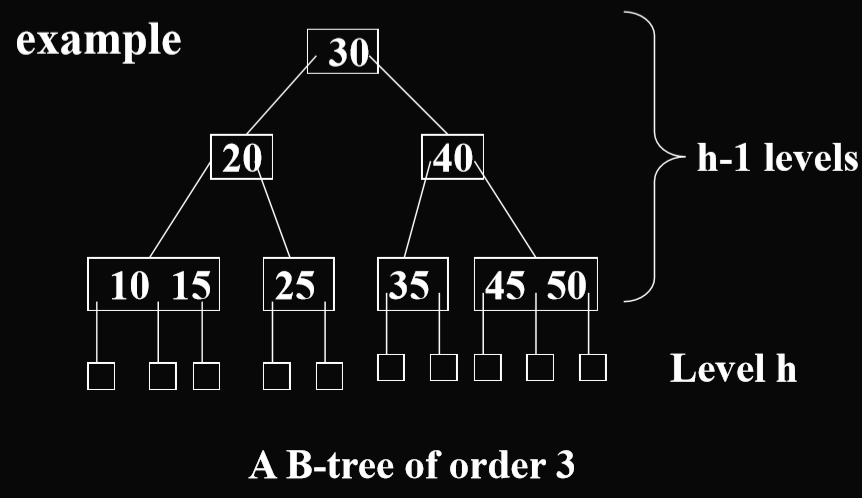
- Eg2. In a Btree of order 3(sometimes also called 2-3 tree), each internal node has 2 or 3 children(在三阶B树中(通常被我们叫做2-3树),每一个内部节点有2个或者3个子女)
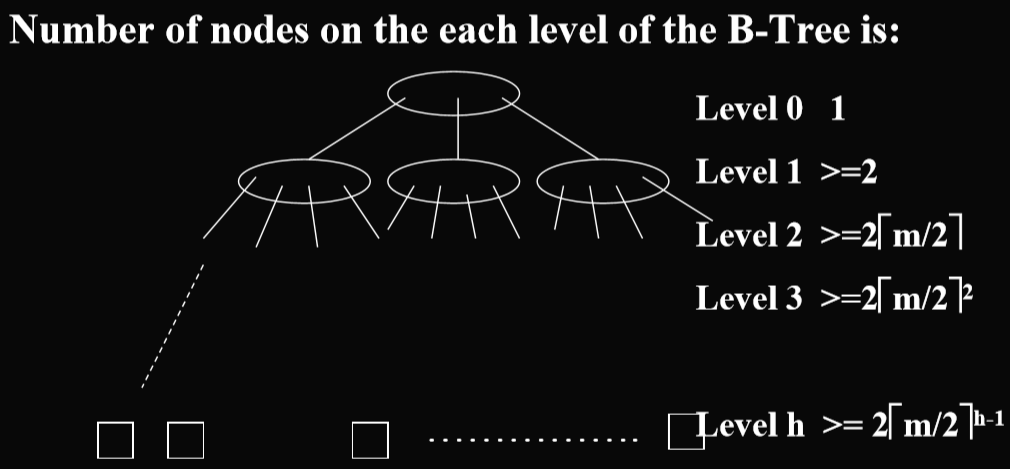
3.2.1. B树性质
- 外节点个数是总共的k值加一
- all external nodes are on the same level(所有的外部结点都有相同的层数)
- number of external nodes = number of keywords + 1(外部节点的个数等于关键字个数+1)
- 证明:b1(第一层节点数,不分内外) = k0 + 1, b2 = k1 + b1,b3 = k2 + b2, …… , 外部结点=kh-1+kh-2+…+k1+k0+1=n+1
- 总的来说就是使用归纳的方法来做
3.2.2. B树搜索算法
- A Btree is searched using the same algorithm as used for an m-way search tree. B树的搜索算法和m叉搜索树的搜索算法是一样的。
- Algorithm analysis:(算法分析)
- the number of disk access is at most h(h is the height of the BTree).(对于高度为h的B树,访问磁盘的次数最多为h次)
- proof: T is a BTree of order m with height h, number of elements in T is n, each time we read a node into memory. The n+1 external nodes are on level h.(T是m阶高度为h的B树,在T中的结点个数为n,每一次我们把一个结点读入内存。那么n+1个外部结点在第h层)
- 考虑最坏情况下的B树的搜索算法
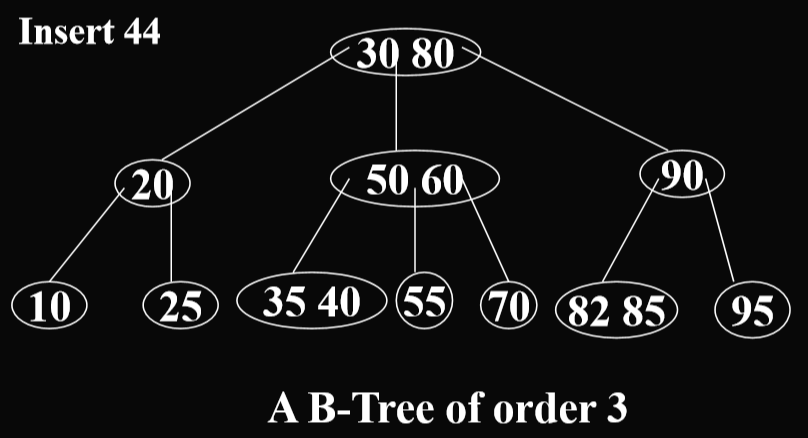
3.2.3. B树插入算法
- B树的插入问题经常发生在外部结点的上一层
算法思想
- 做插入的时候优先插入叶节点:
- 如果叶节点还没有满的时候,直接插入即可
- 如果叶节点已经满了的时候,会进行分类,将中间节点的一个值拉到上级结点(这个结点在中间)。
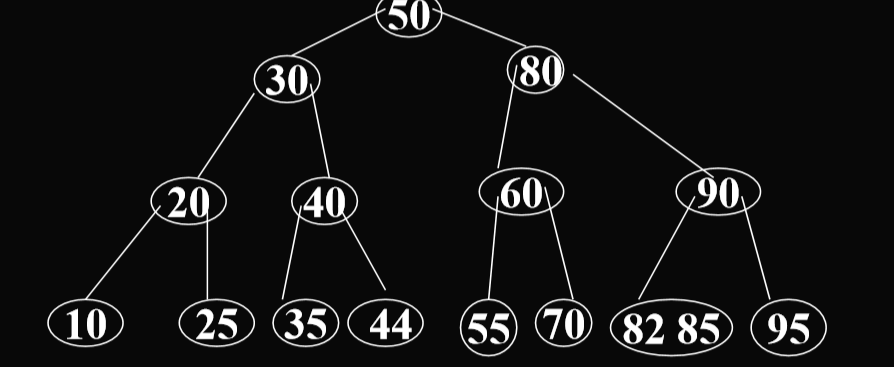
- Insert into a node with m children (also called a full node), like insert 25 into the BTree in the last example, the full node is split into two nodes.(插入到一个有m个子结点的节点中,比如25插入上面那个例子中,满了的节点会分裂成两个节点,就是把中间的提升,将剩下的裂开)
- A new pointer will be added to the parent of the full node.(一个新的指针会被添加指向满了的结点的父结点)
- Because km/2(向上取整) is inserted into parent node, it may cause new split. If the root is split,the height of the tree will increased by 1.(因为km/2(向上取整))
算法分析
- If the insert operation causes s node to split, the number of disk access is h (to read in the nodes on the search path) +2s (to write out the two split parts of each node that is split) +1 (to write the new node).
- 如果插入操作会导致s个结点进行分裂,那么磁盘查找次数为 树高h(在搜索路径上读,查找)+2s(写入2s次的分裂)+1(有可能是创建新的结点,也可能是修改一个节点)
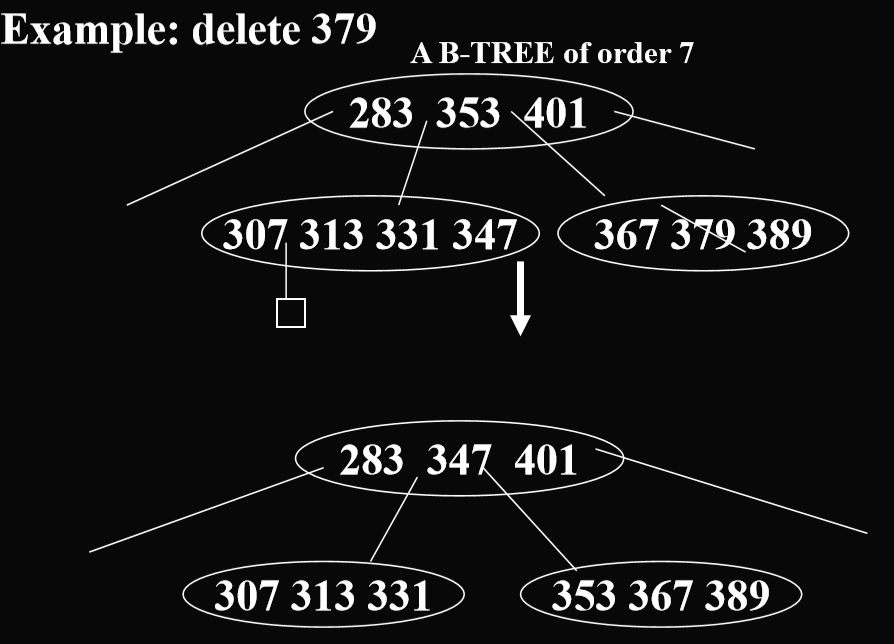
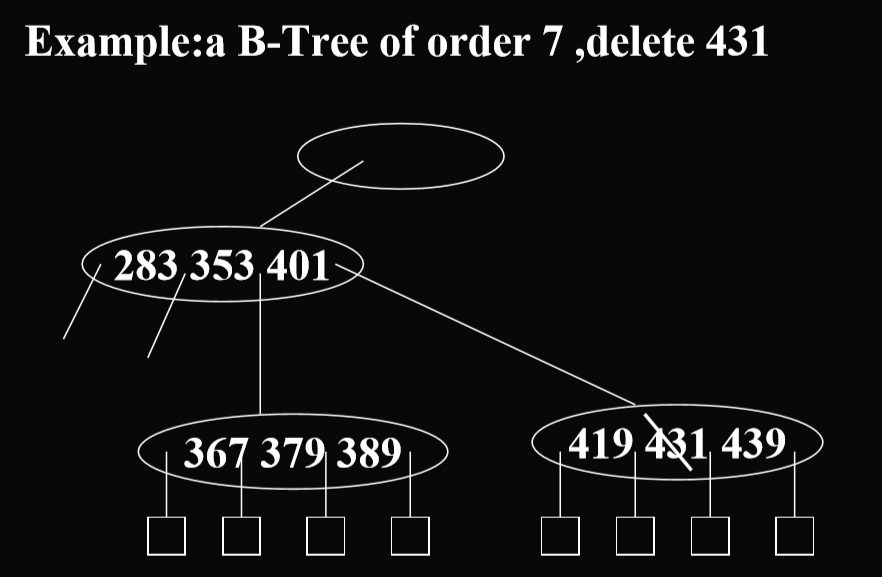
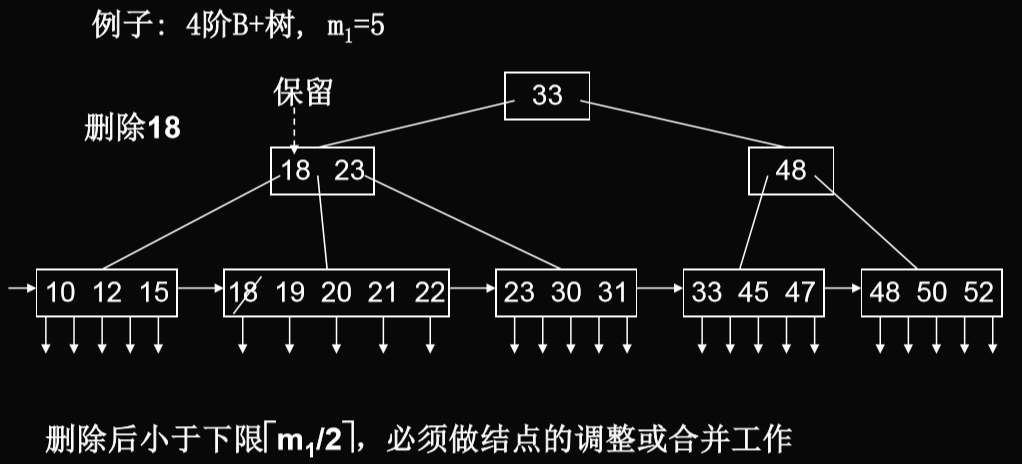
3.2.4. B树的删除算法
首先判断删除的关键码是否都在B树中,不在的话直接退出。
case1:The element to be deleted is in a node whose children are external nodes(i.e.the element is in a leaf)(将要被删除的元素的关键码的子节点是外部结点[小正方形])
- 如果有超过(m/2)(向上取整)个关键码,直接删除
- 如果关键码个数不足(m/2)(向上取整)个,那么向邻居借关键码(也要向上借),如果够借,那么进行调整。如果不够借,那么合并邻居与此节点(还要拉下来一个上级节点的关键码),这样子也可能会导致上级节点的关键码不足,如果根节点合并,则其高度被减少1。
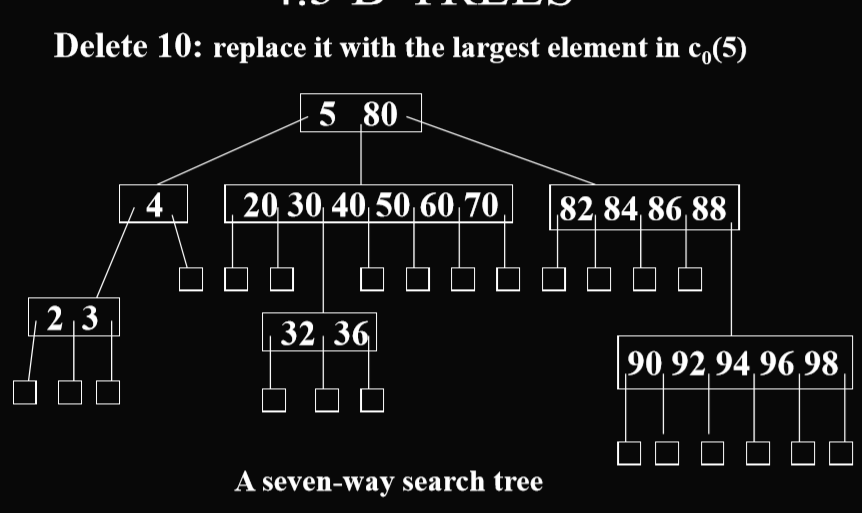
case2: The element is to be deleted from a nonleaf. (要被删除的结点是一个非叶节点)
- 删除这个节点
- 把这个节点替换成右子树中的最小关键码(或者左子树中的最大关键码)
- 因为相当于删除了右子树的最小关键码(或者左子树中的最大关键码),所以重复删除叶结点关键码的操作。
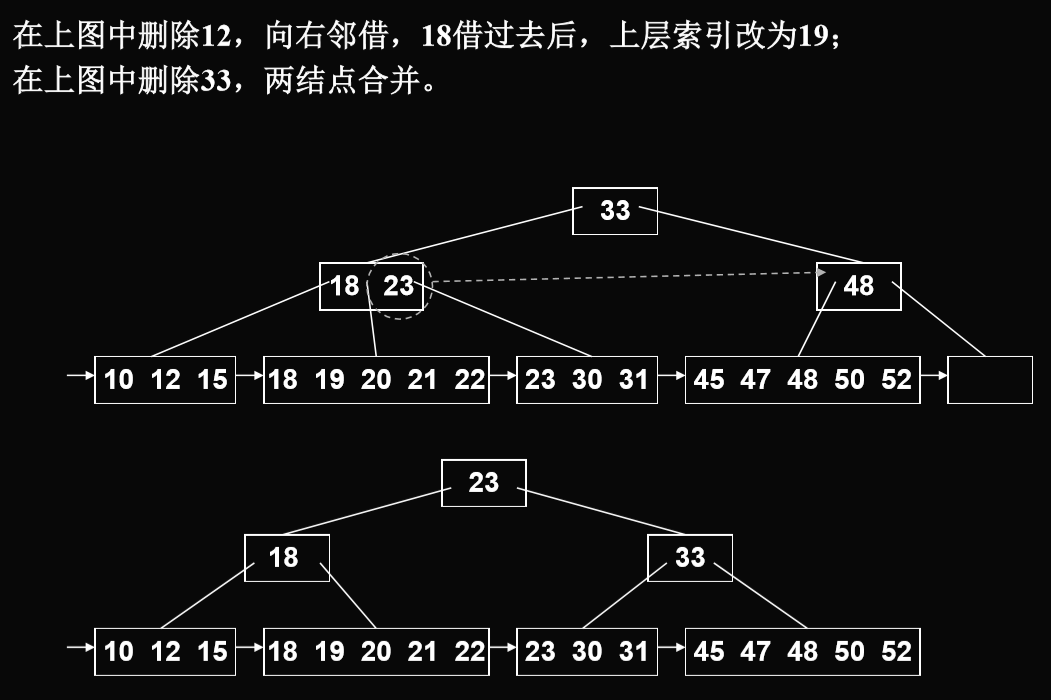
找邻居借关键码的例子:
向邻居借关键码,347 -> 353,353 -> 下面
- 删除后两部分合并的例子:
3.3. B树的实现
- S is the number of elements in the node(是节点的元素的个数)
- ei are the elements in ascending order of key(将元素按照键值升序排列)
- ci are children pointers(子树结点)
4. B+ tree
- 和B树不同的地方:
- 关键码的分布,只分布在叶结点上
- 叶结点的定义,不一定符合m阶,它依赖于关键码字节数与指针字节数而为m1
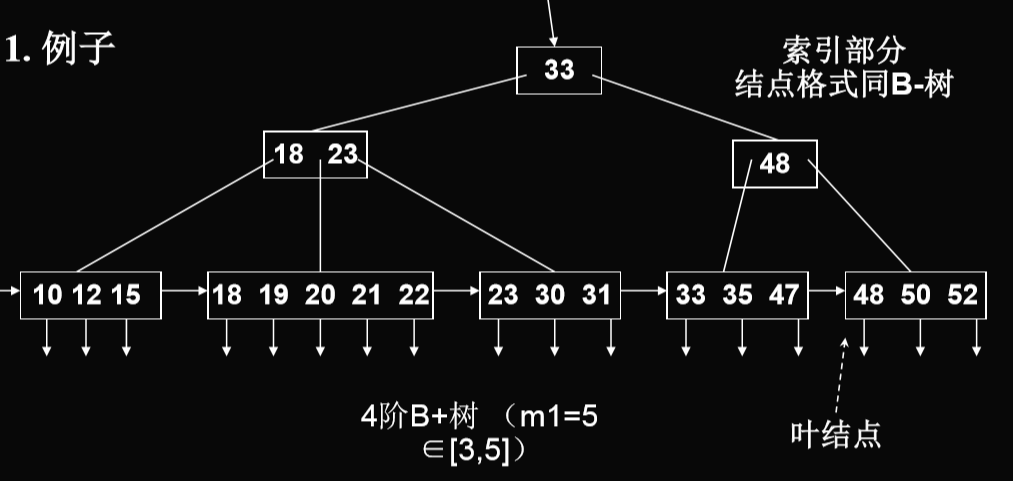
4.1. B+ tree的定义
- 树中每个非叶结点最多有m棵子树
- 根结点(非叶结点)至少有2棵子树
- 除根结点外,每个非叶结点至少有(m/2)(向上取整)棵子树;有n棵子树的非叶结点有n-1个关键码
- 所有叶结点都处于同一层次上,包含了全部关键码及指向相应数据对象存放地址,关键码按关键码从小到大顺序链接
- 每个叶结点中 子树棵树n可以>m,也可以<m。 假设叶结点可容纳的最大关键码数为m1,则指向对象的指针数也有m1,这时子树棵数n应满足((m1/2)(向上取整),m1)
- 根结点本身又是叶结点,则结点格式同叶结点
4.2. B+ tree的特点
- 有两个头指针
- 一个指向B+树的根结点,可以进行自顶向下的随机搜索
- 一个指向关键码最小的叶结点,进行顺序搜索;
- 保证树过深,用来进行平衡
4.3. B+ tree的运算
搜索算法
基本上同B树,所不同的是一直查到叶结点上的这个关键码为止
不会中途停止
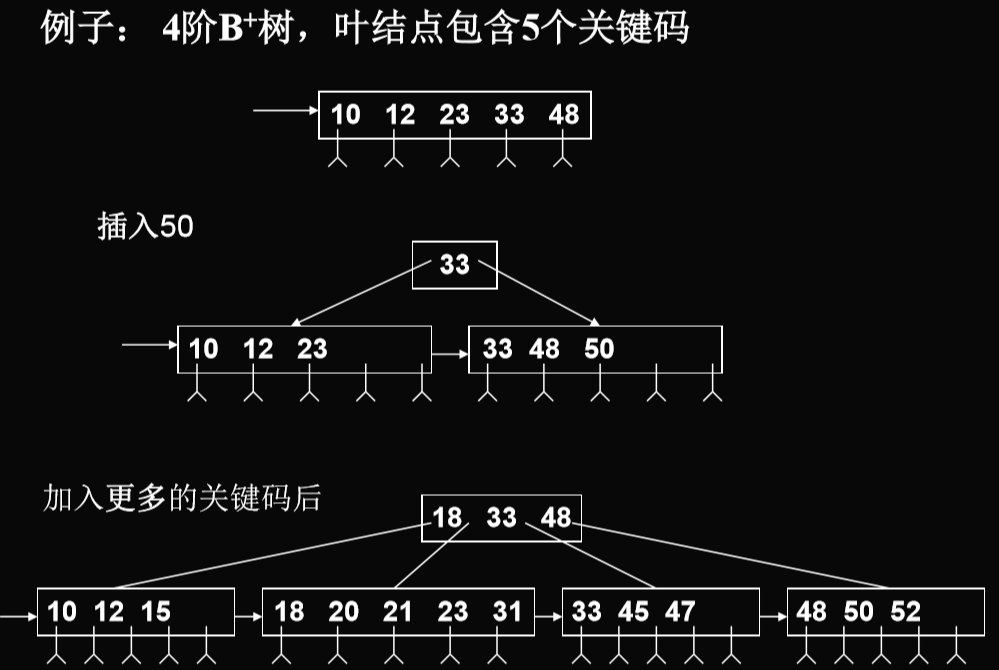
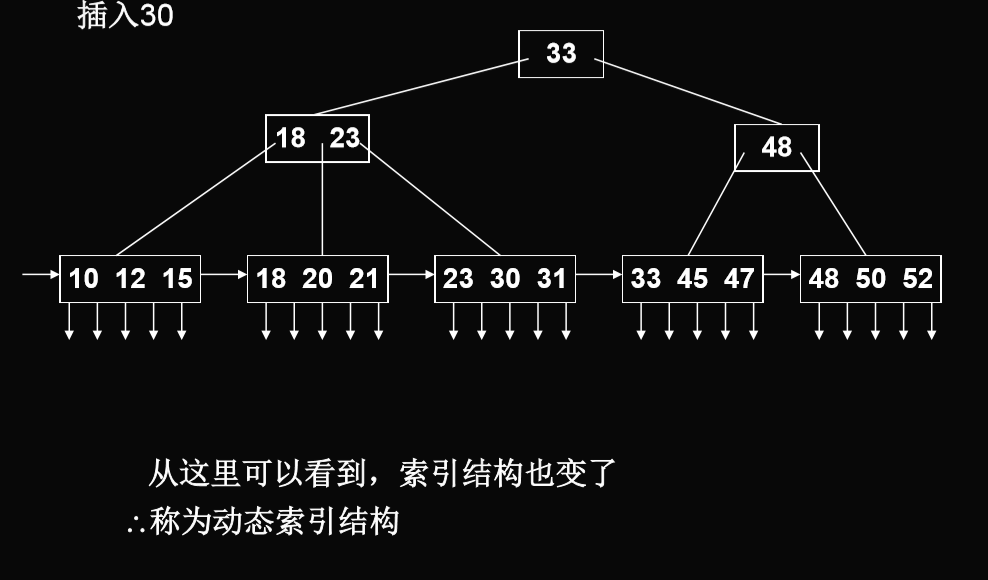
插入算法
- 仅在叶结点上进行。每插入一关键码,判别子树棵树>m1,如果大于,则将该结点分裂:((m1+1)/2)(向上取整),((m1+1)/2)(向上取整)
- 问题变为传递到索引结点上可能的分裂,这时上限以m来确定(同B-树)
删除算法
- 在叶结点上删除一个关键码后要保证结点中的子树棵数仍然不小 于(m1/2)(向上取整).
- 删除操作与B树类似,但上层索引中的关键码可保留,作为引导搜索的”分界关键码”的作用.
5. 题目
- 第9题:
- 邻居的60及它左侧的55被一同借过去
- 20和30成为一个节点,同级的有55,上层50
- 直接删除40,60((50((20,30),55)),80(70,95))
6. 其他参考以及扩展学习